[转]模拟退火算法-TSP问题 - 数学建模社区-数学中国

求某些最优化问题的最优解是一个极其困难的任务。这是因为当一个问题变得足够大时，我们需要搜索一个巨大数量的可能解，从而找到最优的解决方案。在这种情况下，就不能指望找到一个最优函数在一个合理的时间内解决问题，应该尝试找到一个近似解。

一个经典的案例是：旅行商问题( TSP , Traveling Salesman Problem ) ：有N个城市，要求从其中某个问题出发，唯一遍历所有城市，再回到出发的城市，求最短的路线。使用模拟退火算法可以比较快的求出TSP的一条近似最优路径。（和遗传算法求解TSP类似，前面的文章已做介绍）。

模拟退火是什么?
首先,让我们看看模拟退火是如何工作的,以及为什么它是善于解决旅行商问题。模拟退火（Simulated Annealing，简称SA）是一种通用概率算法，用来在一个大的搜寻空间内找寻命题的最优解。该算法是源于对热力学中退火过程的模拟，在某一给定初温下，通过缓慢下降温度参数，使算法能够在多项式时间内给出一个近似最优解。退火与冶金学上的‘退火’相似，而与冶金学的淬火有很大区别，前者是温度缓慢下降，后者是温度迅速下降。我们将热力学的理论套用到统计学上，将搜寻空间内每一点想像成空气内的分子；分子的能量，就是它本身的动能；而搜寻空间内的每一点，也像空气分子一样带有“能量”，以表示该点对命题的合适程度。算法先以搜寻空间内一个任意点作起始：每一步先选择一个“邻居”，然后再计算从现有位置到达“邻居”的概率。

模拟退火的优点
先来说下爬山算法(以下参考：大白话解析模拟退火算法)：爬山算法是一种简单的贪心搜索算法，该算法每次从当前解的临近解空间中选择一个最优解作为当前解，直到达到一个局部最优解。爬山算法实现很简单，其主要缺点是会陷入局部最优解，而不一定能搜索到全局最优解。如图1所示：假设C点为当前解，爬山算法搜索到A点这个局部最优解就会停止搜索，因为在A点无论向那个方向小幅度移动都不能得到更优的解。爬山法是完完全全的贪心法，每次都鼠目寸光的选择一个当前最优解，因此只能搜索到局部的最优值。

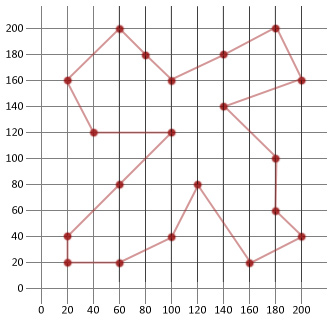
模拟退火其实也是一种贪心算法，但是它的搜索过程引入了随机因素。模拟退火算法以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以图1为例，模拟退火算法在搜索到局部最优解A后，会以一定的概率接受到E的移动。
也许经过几次这样的不是局部最优的移动后会到达D点，于是就跳出了局部最大值A。
模拟退火算法描述：
若J( Y(i+1) )>= J( Y(i) ) (即移动后得到更优解)，则总是接受该移动
若J( Y(i+1) )< J( Y(i) ) (即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）
这里的“一定的概率”的计算参考了金属冶炼的退火过程，这也是模拟退火算法名称的由来。
根据热力学的原理，在温度为T时，出现能量差为dE的降温的概率为P(dE)，表示为：
　P(dE) = exp( dE/(kT) )
其中k是一个常数，exp表示自然指数，且dE<0。这条公式说白了就是：温度越高，出现一次能量差为dE的降温的概率就越大；温度越低，则出现降温的概率就越小。
又由于dE总是小于0（否则就不叫退火了），因此dE/kT < 0 ，所以P(dE)的函数取值范围是(0,1) 。
随着温度T的降低，P(dE)会逐渐降低。我们将一次向较差解的移动看做一次温度跳变过程，我们以概率P(dE)来接受这样的移动。
关于爬山算法与模拟退火，有一个有趣的比喻：
爬山算法：兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法，它不能保证局部最优值就是全局最优值。
模拟退火：兔子喝醉了。它随机地跳了很长时间。这期间，它可能走向高处，也可能踏入平地。但是，它渐渐清醒了并朝最高方向跳去。这就是模拟退火。

接受函数
接受函数决定选择哪一个解决方案，从而可以避免掉一些局部最优解。
首先我们检查如果相邻的解决方案是比我们目前的解决方案好，如果是，我们接受它。否则的话，我们需要考虑的几个因素：
1) 相邻的解决方案有多不好; 2) 当前的温度有多高。在高温系统下更有可能接受较糟糕的解决方案。
这里是简单的数学公式：exp( (solutionEnergy – neighbourEnergy) / temperature )，即上面的　P(dE) = exp( dE/(kT) )
算法过程描述
1) 首先,需要设置初始温度和创建一个随机的初始解。
2) 然后开始循环,直到满足停止条件。通常系统充分冷却,或找到一个足够好的解决方案。
3) 把当前的解决方案做一些小的改变，然后选择一个新的相邻的方案。
4) 决定是否移动到相邻的解决方案。
5) 降低温度,继续循环
样例代码
以TSP问题为例，城市坐标的分布如下所示：

代码以用Java编写。首先创建一个城市类City.java

// 生成一个随机的城市

this.x = (int)(Math.random()*200);

this.y = (int)(Math.random()*200);

public City(int x, int y){

// 计算两个城市之间的距离

public double distanceTo(City city){

int xDistance = Math.abs(getX() - city.getX());

int yDistance = Math.abs(getY() - city.getY());

double distance = Math.sqrt( (xDistance*xDistance) + (yDistance*yDistance) );

public String toString(){

return getX()+", "+getY();

Tour类，代表一个解决方案，即旅行的路径。

import java.util.ArrayList;

import java.util.Collections;

// 保持城市的列表

private ArrayList tour = new ArrayList<City>();

private int distance = 0;

// 生成一个空的路径

for (int i = 0; i < SimulatedAnnealing.allCitys.size(); i++) {

public Tour(ArrayList tour){

this.tour = (ArrayList) tour.clone();

public ArrayList getTour(){

// Creates a random individual

public void generateIndividual() {

// Loop through all our destination cities and add them to our tour

for (int cityIndex = 0; cityIndex < SimulatedAnnealing.allCitys.size(); cityIndex++) {

setCity(cityIndex, SimulatedAnnealing.allCitys.get(cityIndex));

Collections.shuffle(tour);

// 获取一个城市

public City getCity(int tourPosition) {

return (City)tour.get(tourPosition);

public void setCity(int tourPosition, City city) {

tour.set(tourPosition, city);

// 重新计算距离

// 获得当前距离的总花费

public int getDistance(){

if (distance == 0) {

int tourDistance = 0;

for (int cityIndex=0; cityIndex < tourSize(); cityIndex++) {

City fromCity = getCity(cityIndex);

City destinationCity;

if(cityIndex+1 < tourSize()){

destinationCity = getCity(cityIndex+1);

destinationCity = getCity(0);

tourDistance += fromCity.distanceTo(destinationCity);

distance = tourDistance;

// 获得当前路径中城市的数量

public int tourSize() {

public String toString() {

String geneString = "|";

for (int i = 0; i < tourSize(); i++) {

geneString += getCity(i)+"|";

最后是算法的实现类，和相应的测试

import java.util.ArrayList;

import java.util.List;

public class SimulatedAnnealing {

public static List<City> allCitys = new ArrayList<City>();

//计算接受的概率

public static double acceptanceProbability(int energy, int newEnergy, double temperature) {

// 如果新的解决方案较优，就接受

if (newEnergy < energy) {

return Math.exp((energy - newEnergy) / temperature);

public static void main(String[] args) {

// 创建所有的城市城市列表

System.out.println("Final solution distance: " + best.getDistance());

System.out.println("Tour: " + best);

//返回近似的最佳旅行路径

private static Tour sa() {

double temp = 10000;

double coolingRate = 0.003;

// 初始化的解决方案

Tour currentSolution = new Tour();

currentSolution.generateIndividual();

System.out.println("Initial solution distance: " + currentSolution.getDistance());

// 设置当前为最优的方案

Tour best = new Tour(currentSolution.getTour());

// 循环知道系统冷却

// 生成一个邻居

Tour newSolution = new Tour(currentSolution.getTour());

// 获取随机位置

int tourPos1 = (int) (newSolution.tourSize() * Math.random());

int tourPos2 = (int) (newSolution.tourSize() * Math.random());

City citySwap1 = newSolution.getCity(tourPos1);

City citySwap2 = newSolution.getCity(tourPos2);

newSolution.setCity(tourPos2, citySwap1);

newSolution.setCity(tourPos1, citySwap2);

// 获得新的解决方案的花费

int currentEnergy = currentSolution.getDistance();

int neighbourEnergy = newSolution.getDistance();

// 决定是否接受新的方案

if (acceptanceProbability(currentEnergy, neighbourEnergy, temp) > Math.random()) {

currentSolution = new Tour(newSolution.getTour());

// 记录找到的最优方案

if (currentSolution.getDistance() < best.getDistance()) {

best = new Tour(currentSolution.getTour());

temp *= 1-coolingRate;

private static void init() {

City city = new City(60, 200);

City city2 = new City(180, 200);

allCitys.add(city2);

City city3 = new City(80, 180);

allCitys.add(city3);

City city4 = new City(140, 180);

allCitys.add(city4);

City city5 = new City(20, 160);

allCitys.add(city5);

City city6 = new City(100, 160);

allCitys.add(city6);

City city7 = new City(200, 160);

allCitys.add(city7);

City city8 = new City(140, 140);

allCitys.add(city8);

City city9 = new City(40, 120);

allCitys.add(city9);

City city10 = new City(100, 120);

allCitys.add(city10);

City city11 = new City(180, 100);

allCitys.add(city11);

City city12 = new City(60, 80);

allCitys.add(city12);

City city13 = new City(120, 80);

allCitys.add(city13);

City city14 = new City(180, 60);

allCitys.add(city14);

City city15 = new City(20, 40);

allCitys.add(city15);

City city16 = new City(100, 40);

allCitys.add(city16);

City city17 = new City(200, 40);

allCitys.add(city17);

City city18 = new City(20, 20);

allCitys.add(city18);

City city19 = new City(60, 20);

allCitys.add(city19);

City city20 = new City(160, 20);

allCitys.add(city20);

Initial solution distance: 2122

Final solution distance: 981

Tour: |180, 100|180, 60|200, 40|160, 20|100, 40|60, 20|20, 20|20, 40|60, 80|100, 160|80, 180|60, 200|20, 160|40, 120|100, 120|120, 80|200, 160|180, 200|140, 180|140, 140|

和遗传算法类似，该算法也是概率算法，结果为近似和不确定的。

http://www.cnblogs.com/heaad/archive/2010/12/20/1911614.html