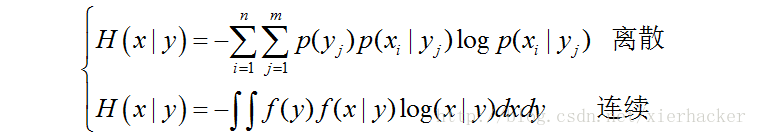
 : ?" k2 {) D/ d/ e- O% _
: ?" k2 {) D/ d/ e- O% _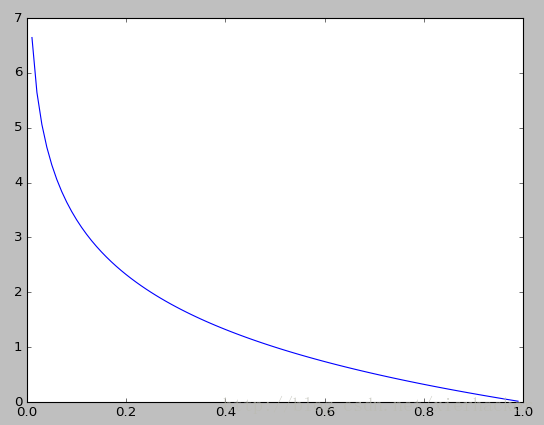 9 n2 F1 K {' F
9 n2 F1 K {' F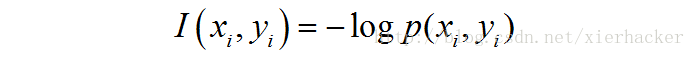 : W4 Y8 c8 W, G/ k
: W4 Y8 c8 W, G/ k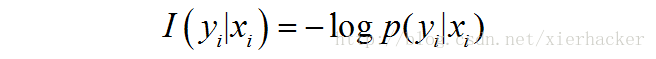 . u2 r2 p5 x0 L% d; g6 s
. u2 r2 p5 x0 L% d; g6 s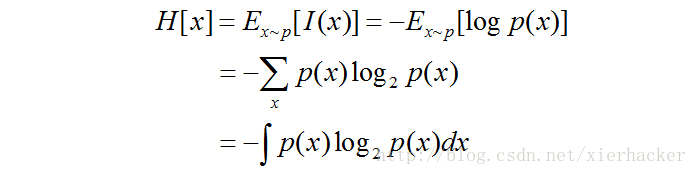
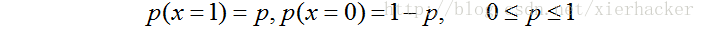 ' _) L8 e8 j4 ~" F% O( z* r2 R
' _) L8 e8 j4 ~" F% O( z* r2 R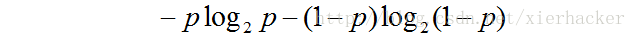 * e3 G2 q! r/ F" Z
* e3 G2 q! r/ F" Z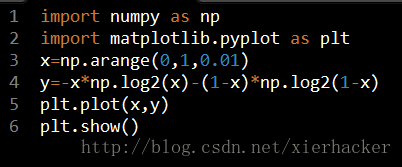 ! r, d9 i& B" {, o$ `$ v! s
! r, d9 i& B" {, o$ `$ v! s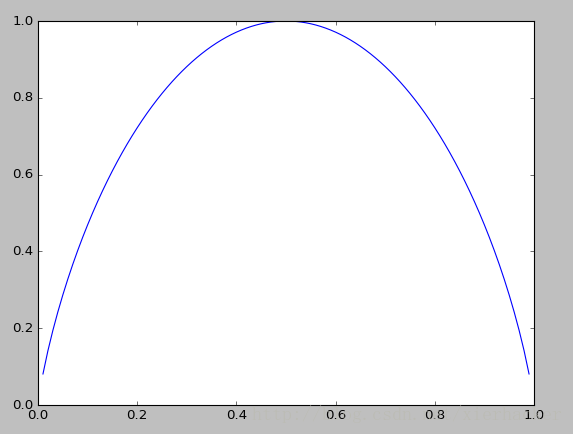
从图中可以知道:
1.当p=0或者p=1的时候,随机变量可以认为是没有不确定性. % {# Z- D8 ^: o# q0 V: o- Y g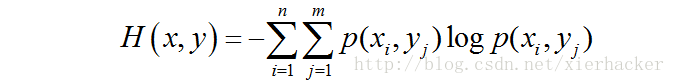
同样,复合熵的公式还可以推广到连续变量和多个变量的情况。这里就不写了。
条件熵:
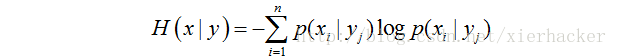 # L' c% S! @# y
# L' c% S! @# y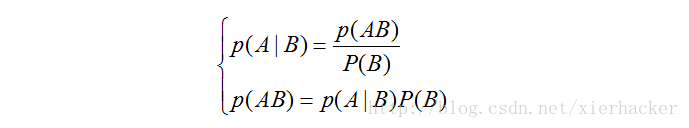
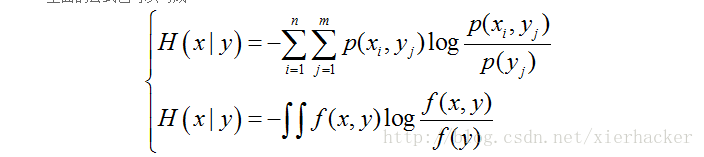 % g" C* \" Z" G, q6 B3 P% g2 e+ v4 V
% g" C* \" Z" G, q6 B3 P% g2 e+ v4 V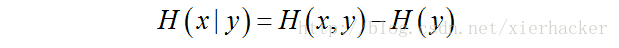 ; |# v& B9 P( I7 n% U! a
; |# v& B9 P( I7 n% U! a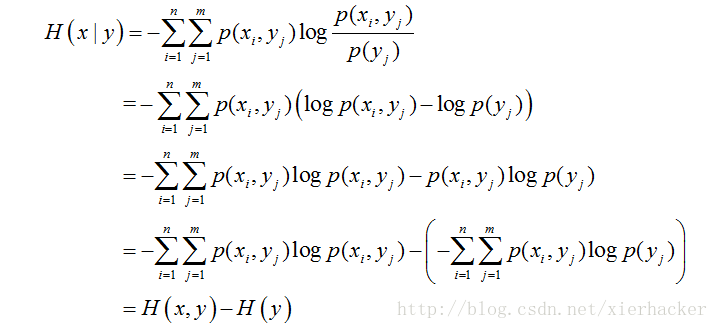
| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) | Powered by Discuz! X2.5 |