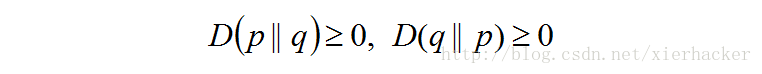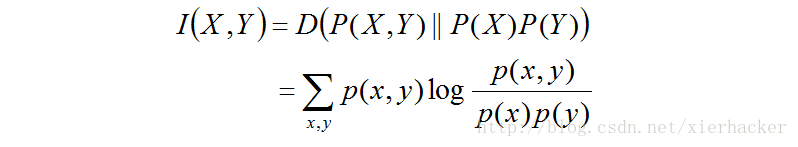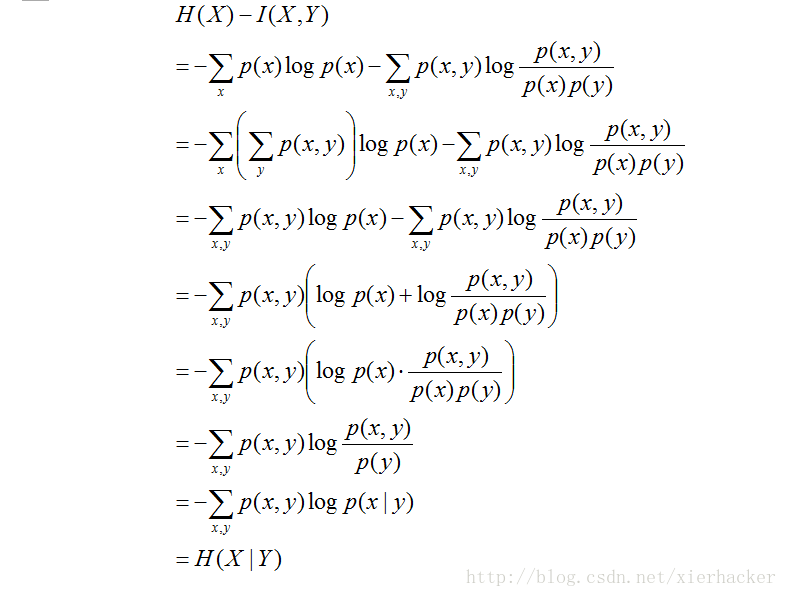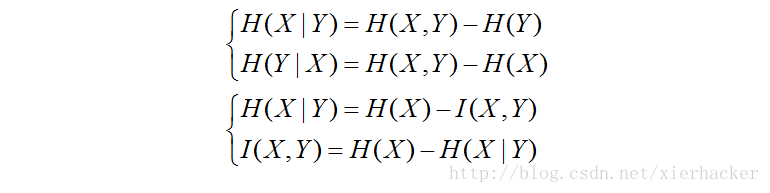数学建模社区-数学中国
标题: 机器学习笔记十:各种熵总结(二) [打印本页]
作者: 重光兰衣 时间: 2018-11-1 10:22
标题: 机器学习笔记十:各种熵总结(二)
机器学习笔记十:各种熵总结(二)二.相对熵相对熵又称互熵,交叉熵,鉴别信息,Kullback熵,Kullback-Leible散度(即KL散度)等。
6 G z% j6 @/ e7 b设p(x)和q(x)是取值的两个概率概率分布,则p对q的相对熵为:
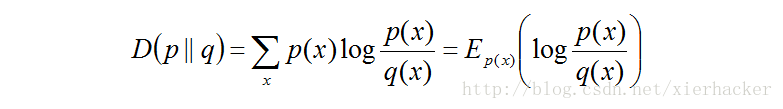
( L) y P6 E: Y4 M3 a# K0 F9 u在一定程度上面,相对熵可以度量两个随机变量的距离。也常常用相对熵来度量两个随机变量的距离。当两个随机分布相同的时候,他们的相对熵为0,当两个随机分布的差别增大的时候,他们之间的相对熵也会增大。 % s& N6 X s% X% V6 P
但是事实上面,他并不是一个真正的距离。因为相对熵是不具有对称性的,即一般来说 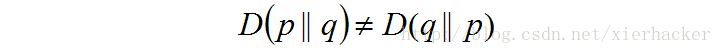 相对熵还有一个性质,就是不为负。
相对熵还有一个性质,就是不为负。
( U& u6 L, E0 u# k; @9 t: F* B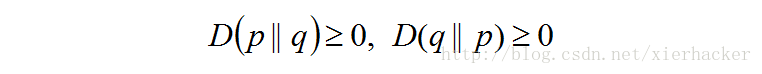
* q/ G8 F F: `! E* P$ T' X# Q三.互信息
: w! O& n/ a; J% u% B y2 X4 ~3 F互信息(Mutual Information)是信息论里一种有用的信息度量,它可以看成是一个随机变量中包含的关于另一个随机变量的信息量,或者说是一个随机变量由于已知另一个随机变量而减少的不确定性。
* M |; Q7 W" W8 B两个随机变量X,Y的互信息,定义为X,Y的联合分布和独立分布乘积的相对熵。 1 p% G. V2 C( D- o
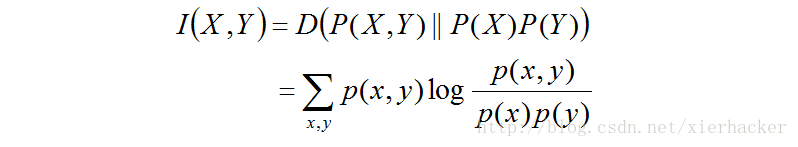
) |1 e0 C! S6 [6 u! x! f; ~6 [4 Y( G( d0 D. _$ p4 K
那么互信息有什么更加深层次的含义呢?首先计算一个式子先: ; Y) O; Q: I. i* k5 F. }; I
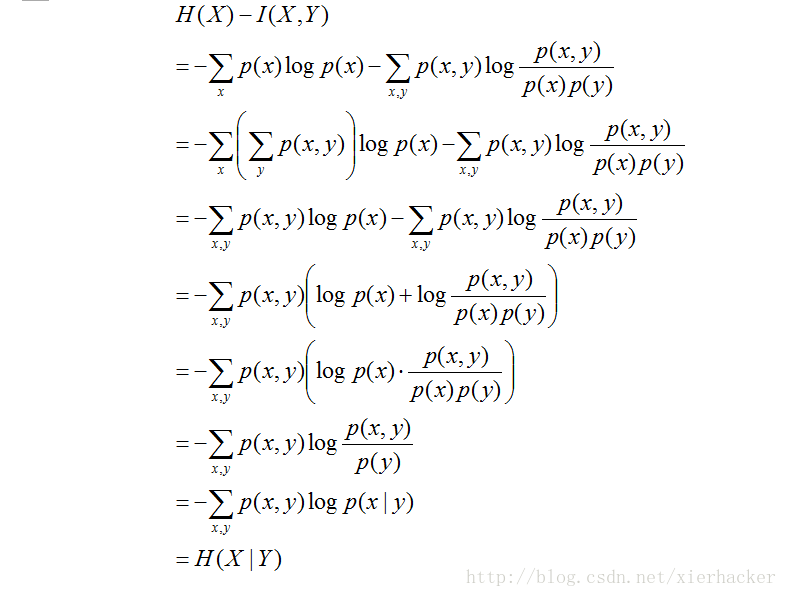
" z& R4 J8 T3 r# R0 V3 ^2 W从这个公式可以知道,X的熵减去X和Y的互信息之后,可以得到在Y给定的情况下X的熵。
四.总结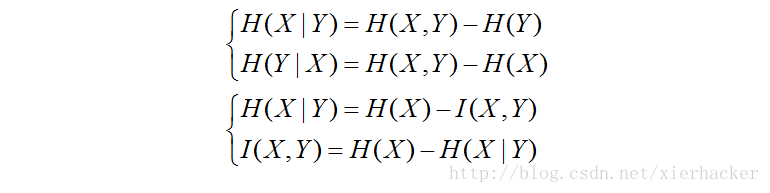
1 ]. \3 t9 J# N$ s3 O" }7 \4 x# I5 v0 c a) j' @8 Z
. w# r l2 M N1 O5 G% A
1 ^9 j3 c4 u' v5 S
| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) |
Powered by Discuz! X2.5 |
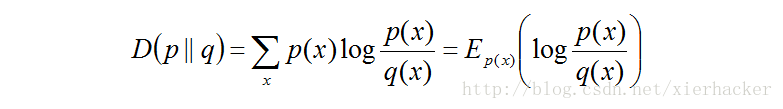
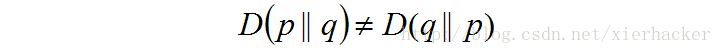 相对熵还有一个性质,就是不为负。
相对熵还有一个性质,就是不为负。