数学建模社区-数学中国
标题: 用Python预测疫情发展 [打印本页]
作者: 浅夏110 时间: 2020-5-15 15:30
标题: 用Python预测疫情发展
什么是传染病动力学?numpy和matplotlib用python实现传染病模型SI模型SIS模型SIR模型SEIR模型
什么是传染病动力学?最近,在报道疫情的众多新闻中,相信大家也看到过一些来预测新型冠状病毒会导致感染肺炎的人数。你一定好奇,这个人数要怎么预测呢?预测人数又有什么用呢?
事实上,从学科方向来说,这类研究属于传染病动力学,就是用数学模型去描述传染病在人群中传播的规律,从而预测患病人数,进而指导政府制定措施和政策去控制传染病的传播。+ X3 b! v: b2 y7 |& Z
这类研究最早可追溯到18世纪Daniel Bernoulli对天花的研究,而我们今天所要介绍的SIR模型是1927年Kermack与McKendrick在为了研究伦敦黑死病而提出的,是传染病动力学中最基础的模型。
介绍了传染病模型的背景信息,不知道现在你对传染病模型更有兴趣,还是执着地对python更有兴趣呢?不论哪种,这篇文章会满足你所有的好奇心。
numpy和matplotlib首先,安装一下这节课我们需要使用的两个python包,numpy和matplotlib。( E+ I1 o$ n3 x1 A2 C$ F! x$ w! m
numpy-是python进行科学和矩阵运算最常用的包。
用numpy建立一维数组,存储和计算每天传染病人数的数据。
! A$ p( ?$ e* j+ x6 i5 G1 Rimport numpy as np
import matplotlib.pyplot as plt
用matplotlib绘制传染病人数随天数变化的曲线,给出模型预测人数变化的直观认识。
好啦,下面开始用python实现传染病模型吧。
用python实现传染病模型为了让大家能够更好地理解,我们先不直接说SIR模型,我们从最简单的开始。
SI模型首先想象这样一个场景,一个城市有 个人,假设没有人出生和死亡,忽然有一天有 个人感染了病毒成为了患者,如果每天每个患者能够有效传染 个人,那么第二天患病人数是多少呢?最简单的答案是: ,也就是说每天都会新增 个患者。那这样以来,在无限远的将来会有无穷多的人被感染,显然这是不合理的,那错在哪里?仔细思考,你一定发现了,已经患病的人就不能再被传染了,所以我们有必要把人群分为两类,易感者(S-susceptiable)和感染者(I-infective)(你猜的没错,这就是SIR中S和I的含义,R的含义之后介绍再讲)。为了之后方便计算我们记易感者和感染者在人群中的比例为 ,那么 。我们重新考虑上面的问题,顺便来个示意图:
 Image Name这样的话,每天新增的患者数为 ,也就是总传染人数乘以易感者所占的人群比例。
Image Name这样的话,每天新增的患者数为 ,也就是总传染人数乘以易感者所占的人群比例。
4 H$ S- O+ J" ^, v那么每天的感染者比例的增加量就是 。我们假设城市有一千万(N=10的7次方)人,每个患者每天接触感染每天0.8人(lamda=0.8),初始感染人数为45人(i0 = 45/N),我们来模拟70天(T=70)的情况。
# population
( g$ t0 @$ u( |2 \- N1 @N = 1e7- U: ?- T$ Z! R+ E! q
# simuation Time / Day
- B6 O" A- |' Y2 c" zT = 70
' i, V2 I: @* ?; _1 F) H, \# susceptiable ratio
4 B. }8 y5 a$ [( @s = np.zeros([T])
9 P6 k: y4 ^" v7 o N# infective ratio% a4 j, u/ F- j% W( }/ \" N5 j' A
i = np.zeros([T])
* h5 w$ ?" _' H" `* n# contact rate
5 Z; d$ d" k* A7 v2 r# F d0 Slamda = 0.8
, ~" F+ j: Y7 Z: S7 T8 ?& ^5 U3 x& p1 c
# initial infective people
+ u1 i/ d, t. t5 u# l. ki[0] = 45.0 / N
& I6 D2 ^ i, J8 A s3 ?* Z! [- w" ^
/ m3 |9 o* t" \1 p; G5 ]for t in range(T-1):: z7 q' L. D% G
i[t + 1] = i[t] + i[t] * lamda * (1.0 - i[t])+ Z A# f, h5 T! z% Y' A
0 L; a) t: k E
" B$ S' X1 @3 I+ W# \, \6 N9 b$ M
8 }" Y! O- M2 ^6 {0 |7 U# N相信其他语句大家都明白,新知识是这两行:. G9 _: F( r! ~; i# a. g
0 I1 x% r& B, r: g& D) C1 n! q4 Q5 g v4 N3 c
s = np.zeros([T])6 R8 x0 q) y2 ^' V
i = np.zeros([T])
5 v& E( |+ @9 v* J( s* A# o
$ U5 S) F' H# U4 W* V) q( q这两句话的意思是一样的,就是利用numpy(已被我们重新命名为np)的函数(zeros())来建立一个所有元素都是零的数组,而给的参数决定了这个数组的维度。比如:
- _# W$ z) U- o) y% g+ X J! `7 {) C* I2 H% t
a = np.zeros([2,3])
: [8 F% p) B W1 ~8 ma/ v% H7 p1 c4 N) w7 S
9 u4 R4 ]7 j# K6 n: I6 h+ oarray([[0., 0., 0.],4 F; z+ [/ Q! m) P, e
[0., 0., 0.]])
: s6 w+ Z5 g: X' B. a8 Y7 v
: k$ U) w5 ~, h# Z+ C
Q) T# [, v' M k% U. Uarray([0., 0., 0., 0., 0.])
- P7 Z3 c8 W N( I; z- i1 ~" M% \+ `$ Q, J/ _7 l' W
I9 m: H! u. M a9 a类似的还有产生元素全部是1的数组的函数np.ones():2 C/ H v% T+ T8 K" x, S
0 I7 i9 o l& O+ a! ?9 z! X3 \. \6 ca = np.ones([5]). ?& y+ y7 I5 J9 }2 N
a
3 ]+ e. @7 k4 B8 D/ u
; C5 J( e5 D$ l1 J$ Karray([1., 1., 1., 1., 1.])
3 M9 Q& V8 I& p" j+ m+ E3 D2 W" x) O; B$ j1 p& k5 v! D" c
$ q& o5 q- [1 a- q9 z4 B- o
a = np.ones([2,3])
0 v) t& p3 _% w7 aa
% a+ F! ~% y9 X! e- V
/ ?6 }! V0 }% f4 C+ D7 ]/ a) Y9 X8 X. T5 M- K& u
array([[1., 1., 1.],- i+ ]! D* b/ {4 \/ j) H3 h
[1., 1., 1.]]); N2 q6 S. ?, |4 H& s
?- d% T0 `+ S% r7 w% w+ ~' }
' c( N/ }2 U9 V. S! {& D" x4 P; B) ~( ]plt.plot(i)5 V. a/ x2 w$ R4 h
) `) ?) L' y$ R) K# q+ u& D6 ~+ ^( o& O& @
[<matplotlib.lines.Line2D at 0x7f0c2768d6d8>]' N- V! ?# j( w1 w5 t
2 B6 N+ \# W$ p
3 V2 Y! A3 U' T. n* ?4 K2 i# |& |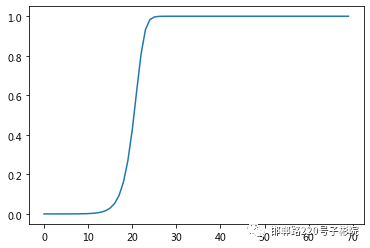
: V6 S, S+ g& Z8 _: a, C, W/ i1 t) z2 [% H3 `8 F
* o$ g/ a ?: a1 \! y# @实现SI模型的核心代码是第三个cell的第11,12行:
) H, P3 x8 o6 Z9 h* i# U' S3 }; o# X" c
for t in range(T-1):5 B9 q% Y6 g. U$ T+ h4 T
i[t + 1] = i[t] + i[t] * lamda * (1.0 - i[t])
+ T% M5 D: A) L
/ k9 ?4 V) D3 L就是我们建立的数学模型,利用python的for循环语句累加迭代的方式把每天的增加量叠加到感染者比例上。
运行代码完成计算,我们利用matplotlib的pyplot来画出感染者的随天数的变化曲线:
' ^9 q2 L, H2 M5 U
fig, ax = plt.subplots(figsize=(8,4))
) a; z; b+ j `0 nax.plot(i, c='r', lw=2)
: ]3 X4 U ^+ O. Eax.set_xlabel('Day',fontsize=20)
1 ~7 X2 l0 t% r3 }$ aax.set_ylabel('Infective Ratio', fontsize=20)# U- U- ?6 n( z
ax.grid(1)
3 [7 f ~: u% i1 nplt.xticks(fontsize=20)3 `3 K- `9 l" ?5 B
plt.yticks(fontsize=20);# X# H, X; `' F
0 m9 `& L) w. z1 |) v
: t: G- p c t& l: M! P: [) q" s& N. e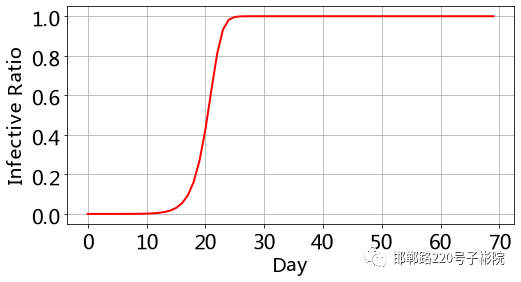
' v% z6 |( T5 O! N4 S+ T l' u. a+ \6 B! w
从这个结果看到,大约在25天左右,全部人群都会变成感染者,感染率 。
: I9 Y7 X7 u7 ?% ^在程序中我们假设每天每个患者传染0.8个人,你可以改变lamda的值,观察全部人群感染的天数的变化。/ y- _2 {) E8 T
认真思考你会知道,lamda的现实意义就是该城市的卫生水平,衡量的是消毒,隔离这些措施执行得怎么样。回到传染病模型,按照SI模型计算的结果,我们全人类都会患病,这好可怕!原因是我们忽略了一个很重要的因素,那就是我们有奋斗在一线的医护人员,我们会被治愈!所以SI模型只适合研究具有高传染风险又不能被治愈的病(比如HIV)。
但是对于其他病,我们是可以靠医疗和自身免疫系统康复的,那么紧接着的一个问题就是,被治愈后还会再被传染上嘛?根据这个问题的回答不同,我们有了两个不同的模型,SIR 和 SIS。现在可以揭晓,SIR的R的含义了,就是移出者(Removed),现实含义就是指被治愈后不会再被感染的人。而SIS表示治愈后仍然还是易感者。下面我们用python来分别实现这两个模型。
SIS模型为了实现这个模型,我们需要引入新的一个参数,治愈率 。好啦,先上我们的新示意图: Image Name和SI模型做比较,区别就是计算感染者的增加数时要减去被治愈的人数。
Image Name和SI模型做比较,区别就是计算感染者的增加数时要减去被治愈的人数。
4 ~+ H( I4 V; }( V; N3 l所以这时候每天的增加的感染者为: ,2 A8 K p0 c' A, `
增加的感染率为: 。
. C2 c! o$ `* y3 L# i% u& t2 _& A* r模型完成啦,修改python代码:
8 k' r8 d/ m5 H. u# susceptiable ratio
y. U* o# k4 ?4 x7 is = np.zeros([T])8 i3 s5 J& A/ l& I( {, B1 p
# infective ratio5 F/ a* [8 Y- G, ^3 D4 N) X
i = np.zeros([T])
; ]" C8 O/ n) r9 h0 o0 X$ q
$ C3 w% g4 ~" a% X2 i9 |. I# contact rate
1 [6 Y5 P1 D! t, _/ K* `lamda = 1.0* f& A) i7 m. M0 ?
# recover rate
# v0 M9 x* J4 j8 y7 ~8 x2 u+ Qgamma = 0.5 1 x- H. w& a4 U+ Z4 {6 z1 \) A
. _/ W6 C* ]4 V1 r5 j
# initial infective people3 f2 K1 ?, |+ z; a: }5 W
i[0] = 45.0 / N
( u& U' S- _4 A! V, e6 R7 V% g! v+ r! r+ _' S
for t in range(T-1):
3 _) S- b+ ?/ K3 n1 b i[t + 1] = i[t] + i[t] * lamda * (1.0 - i[t]) - gamma*i[t]
* e. k+ g/ \. `' h0 n) l
2 h1 C: O& S' ]# `1 a% f) U! u2 D( @6 S1 @3 ]* J
' T0 y5 s/ B$ }5 E' }运行代码,我们画出曲线(代码和SI模型的画图完全一样):9 J4 Z/ K1 _- W* ^
$ b f$ E. y U1 }
fig, ax = plt.subplots(figsize=(8,4))
2 F# J6 W6 C. A: X& S# `ax.plot(i, c='r', lw=2)( k) F4 l+ o; U& n/ T
ax.set_xlabel('Day',fontsize=20)* t3 `$ U* t9 Q7 X0 n
ax.set_ylabel('Infective Ratio', fontsize=20)
" F$ @- f/ F5 a% k& `0 W( z, Nax.grid(1): Y4 i4 `1 i: {- T+ y; e
plt.xticks(fontsize=20): \% I b7 H% B
plt.yticks(fontsize=20);- i4 ~' I7 L% r0 P1 I
# R- F# a" H" l4 F
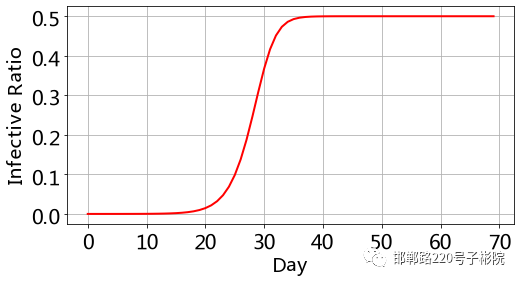
% P$ B' V7 A2 O- M* s& S& k& n8 D' d) W+ |. c
! U! [) \5 Y. _6 d' n; W' V行代码,我们画出曲线(代码和SI模型的画图完全一样)
# n& p. x8 B6 ~; [可以看到,达到最大感染率的时间退后10天左右,最后感染和治愈达到动态平衡,人群中有始终有一半的人感染着。所以,SIS模型适合研究具有传染性和反复性的流行病,比如常见流感。同样的,感兴趣的话,改变lamda和gamma的值,观察曲线的变化。和lamda不同的是,gamma的现实意义就是对这种疾病的治疗水平。
SIR模型加入了移出者,被治愈的病人不会再被传染,先上我们的新示意图:
 Image Name
Image NameSIR 模型$ L3 b: `$ y0 @ W
注意到这里,人群被分成了三类,不再只有I和S,所以相比于之前的模型,我们需要找到新的约束关系。现在我们需要分别计算三种人每天的增加量了:
* m' y2 Z- h' `# _+ d. p( g) g$ {' B- 易感者:每天都在被传染,所以一直在减少,减少量为被传染的人数:
- 感染者:增加了被感染的人,减少了治愈的人:
- 移出者:增加了治愈的人: 9 u: ~. {$ L7 j9 y8 x5 @
建模完成,修改python代码,并且假设人群普遍易感,新型疾病,初始没有移出者。
, P8 P' W R4 d& C7 m/ S( |
# population
8 x0 e6 ?9 X+ A1 u* t! m* CN = 1e7 + 10 + 5
* C7 y" E* M1 R/ e: o% V# simuation Time / Day
) F Q2 D' C( sT = 170
, X0 p5 I( n% J7 ]# susceptiable ratio% `- m& {9 H+ i$ N
s = np.zeros([T])3 F {' p8 y$ O: C* [# e
# infective ratio, M e$ b6 I6 m0 k5 E
i = np.zeros([T])
+ c/ M% F/ L+ n/ K$ k/ ?9 {# remove ratio1 d( \7 u- {5 ^. \
r = np.zeros([T])# M) T0 w! j& Y8 T: q) d* \
; C9 f% ^5 z' l
# contact rate
, h3 j, O% g" @5 _% h/ Tlamda = 0.2586( y9 t3 x4 a& D
# recover rate
/ O2 [) n5 W z3 n9 r4 Dgamma = 0.0821
8 Q9 `% u- B. M$ d. u
$ n6 M/ f- P; L# initial infective people
4 L. c/ S% V+ R8 c$ M2 R) a( ni[0] = 10.0 / N
6 T& o& V, x; P/ {# v, P5 X% n1 Ns[0] = 1e7 / N
5 @5 _8 s( T( g: ofor t in range(T-1):
" i* e* K, ]7 {0 Y i[t + 1] = i[t] + i[t] * lamda * s[t] - gamma*i[t]
6 ]6 V5 T0 Y- B7 ~$ s2 _" r s[t + 1] = s[t] - lamda * s[t] * i[t]
- w$ n+ D4 f/ J- \ R* O r[t + 1] = r[t] + gamma*i[t]
- {/ Z9 S, _% Z; l% T/ t9 i5 P+ J! b1 ?" L; M
fig, ax = plt.subplots(figsize=(10,6))
' }, t* P+ ^6 y7 y; J: |ax.plot(s, c='b', lw=2, label='S')
' z4 d2 j) R- F3 l' D, {ax.plot(i, c='r', lw=2, label='I')
; t: S, R! l3 c+ E5 F2 G/ `ax.plot(r, c='g', lw=2, label='R')8 Y! Q6 e- b1 Z. I& `4 B( O
ax.set_xlabel('Day',fontsize=20)
+ ~7 o9 M$ e1 x8 d$ pax.set_ylabel('Infective Ratio', fontsize=20)4 _) X0 S! w8 }* K8 ?$ p4 b& `5 G
ax.grid(1)
% g9 ], D! F; `; b* Yplt.xticks(fontsize=20)1 ^( J' T0 v7 ]
plt.yticks(fontsize=20)
1 | X) K0 W5 X' X w6 ]plt.legend();( R: ?! r0 f, o( {6 q7 R$ u
0 k. b6 e6 A+ E4 C, c
. E3 t8 O+ u; T, L , e7 m: Q& x( K! l0 G- U
, e7 m: Q& x( K! l0 G- U
9 i) S t6 ]/ R' o感染人数峰值发生在一个月左右,最大感染人数不到人群的20%, 但是最终人群的80%都会得此病(就是最终的移出者的比例)。SIR模型适合研究没有潜伏期的急性传染病,治疗后能够痊愈并具有抗病性。
到这里,虽然不准确,我们也可以先用SIR模型来分析一下此次疫情,武汉新型冠状病毒的传染病动力学!
模型有了,其实就是确定参数的问题。一开始就有人做了这个工作:
 Image Name于教授给的参数是参考了非典的, ,初始易感人数为一千万, 初始感染10人,初始移出者5人,那么我们的城市总人数 , 带入我们的模型得到结果:
Image Name于教授给的参数是参考了非典的, ,初始易感人数为一千万, 初始感染10人,初始移出者5人,那么我们的城市总人数 , 带入我们的模型得到结果:重现于教授的模型7 G. o* b: o l6 q l
高峰和尾声日期的推测基本相符。
: B$ s% z2 A* s% ?$ B# @) C0 ?# susceptiable ratio
4 ]% v6 ?" j& I4 q O/ _ Ks = np.zeros([T])
$ j8 _* b5 u" X- t, @9 s# M# infective ratio
7 p& E) Q" y4 L, e; m; e# Ei = np.zeros([T])4 {+ I8 u( O- G5 w. H: ?
# removed ratio
$ `% d. @( ]% u' _r = np.zeros([T])7 h) ~( l% T f, y; T
2 |% I% ^) J. t- S# birth ratio
& ^9 K+ B( g) u o& hb = 20.0 / N
' Y+ r% x( _4 U4 q# death ratio2 n& N' K3 Z8 }
d = 10.0 / N
* t" S. [9 B1 F+ }
3 s0 B% Y/ o9 j0 e# contact rate. E5 u: ~& T& H( x3 n9 S
y = 1.5% Y' p* w0 @0 D' I
# recover rate
7 h/ e( z: v# X! r3 L: `3 O' lu = 0.8 # 1 / infective_period2 h) N) }' g; }" G, x
/ \; ]8 _3 y% W, W* [3 l# sigma = y / u4 i% G7 I* k5 R# g( \
- S- W8 I/ k. C
# initial infective people
( `7 q& G% J+ N' Gi[0] = 45.0 / N1 G% Y& d9 u. ?
s[0] = 1 - i[0]: R% K( i1 N: F% f1 _
for t in range(T-1):+ {8 J8 G3 k( Q+ X* b& F
i[t+1] = i[t] + i[t] * y * s[t] - u*i[t] - d*i[t]( v' [" p$ a( d+ \7 O) ^' I+ `
s[t+1] = s[t] - y * s[t] * i[t] + b - d*s[t]5 s* i4 o' b9 U3 t- e) K' e# P3 {2 `5 `
r[t+1] = r[t] + u*i[t] - d*r[t]& J7 J, z) E% X# z+ `
- V& c. e( \4 S$ X* x8 K" F
plt.plot(i)( D+ H- D8 u6 q8 Y G
plt.plot(s)8 v9 w, `' Y8 C
plt.plot(r)/ ]; {) M% T9 S
plt.plot(np.diff(i),ls='--')( g; K" ?& Z6 W* I2 N
7 f" l# e# P) A3 l6 F, J; d R+ {2 E2 Y9 x: h }4 f
[<matplotlib.lines.Line2D at 0x7f77796e8518>]
) C/ @9 d) p3 k7 y+ ]' b$ f' @( Q, L8 \
 ( _1 a: w8 ~' |, R8 h; `- _7 v
( _1 a: w8 ~' |, R8 h; `- _7 v
2 z/ W8 I( l+ ?! X1 t
SEIR模型但是,SIR模型和实际情况的出入会比较大,因为忽略了太多因素了,比如说潜伏期,比如说政策调控,药物,出生死亡等等。下面我们可以和前面一样,把潜伏期考虑进去,新增一个人群,叫潜伏者E(exposed):
 Image Name
Image NameSEIR模型
, }4 }+ h- }" |4 `同样的我们需要计算各人群每天的增加量:
S:每天减少: : F) T, o2 L' p+ ]
E:每天增加传染,减少发病:
8 G( d7 {4 n# J9 bI:每天增加发病,减少治愈: ' E( b4 _1 `5 k6 _' q- R% \2 v
R:每天增加治愈:
, E e5 h4 Z( t0 @2 ^; U建模完成,修改我们的python程序,这里的 可以理解为潜伏期的倒数。给的4天。新型冠状病毒给目前临床的潜伏期是3-14天。; n! w; o! N, z. \ @: I
# population
- ]% A! G" K( T( ] {% ]9 YN = 1e7 + 10 + 5$ X4 W% a" z& f2 d
# simuation Time / Day0 u) ]/ R* X1 j+ p2 k! U" J( U
T = 1708 t5 F$ V* z/ p+ }' D! F& m: l
# susceptiable ratio
) z- a1 ?- b% v. W2 P3 `s = np.zeros([T])
: X/ D: {% O% b3 e) O# exposed ratio7 B+ V! P8 ]+ q O! N8 Z- w4 j
e = np.zeros([T])
6 P8 v( h7 E* c4 m# infective ratio* O0 V" a% T( `) P4 U
i = np.zeros([T])1 ]. D' R; P6 |- N
# remove ratio
% t9 {1 [' \; e( T, Z( Br = np.zeros([T])
+ z8 V+ f; G6 O- e8 e1 v
. e2 }, E6 x1 U9 p( A9 V" q& @; d' }# contact rate
: b/ {5 M4 k1 n1 h+ z/ klamda = 0.5
t+ |6 l, z/ u% ?1 j/ o# recover rate
1 W+ R C* L, _$ F2 c" E7 I. D. vgamma = 0.08219 k4 O6 c9 g8 c& V' {. z
# exposed period3 \ P5 v9 i/ u
sigma = 1 / 45 d, u% R- K6 }
: A4 ?; \. L: P% O# initial infective people5 W, W, S" M9 ], P# J4 R& K) Q
i[0] = 10.0 / N
( k9 H/ [$ ?5 _( }" I! ds[0] = 1e7 / N
0 ]4 |* t9 {! h& p5 \* A fe[0] = 40.0 / N# [, D% @5 v% @; V3 J4 i
for t in range(T-1):& L) q# Y0 j, S; Q7 a1 c( s3 ~+ S
s[t + 1] = s[t] - lamda * s[t] * i[t]
+ z7 m9 Q0 l) A% B e[t + 1] = e[t] + lamda * s[t] * i[t] - sigma * e[t]
7 d& C: G, q3 I- B' ?% _0 ]. a i[t + 1] = i[t] + sigma * e[t] - gamma * i[t]
8 y8 o# k* [) a- W6 w r[t + 1] = r[t] + gamma * i[t]
' g4 P; C7 }/ W. e" S; L8 K- L9 E3 q% j
_ D c* A- d3 r% e, w
fig, ax = plt.subplots(figsize=(10,6))
5 T/ K `, n, C Z3 W( |- jax.plot(s, c='b', lw=2, label='S')
$ O% M1 t% M3 x3 _ax.plot(e, c='orange', lw=2, label='E')
) V" F) C* o# R8 i/ `/ m! _( e1 vax.plot(i, c='r', lw=2, label='I')* {6 T1 D/ [- R. u3 U8 h' s
ax.plot(r, c='g', lw=2, label='R')
8 }+ F0 x, P% H% q2 K( C8 Bax.set_xlabel('Day',fontsize=20)9 K' a1 `2 \0 U7 Z) T7 ^
ax.set_ylabel('Infective Ratio', fontsize=20)
& _( `3 d: y, s& D+ [- o9 ?ax.grid(1)
. }# [' X S0 e9 U9 S+ G8 aplt.xticks(fontsize=20)
' Y5 J7 A; ] M. yplt.yticks(fontsize=20)
+ ^! K |& s, |+ [1 @plt.legend();, p' N, m R1 m3 @2 Y" r5 b" k
+ K7 Q+ t- V$ K* A3 `
- Q; j' U1 e. _3 V, N- g( s+ F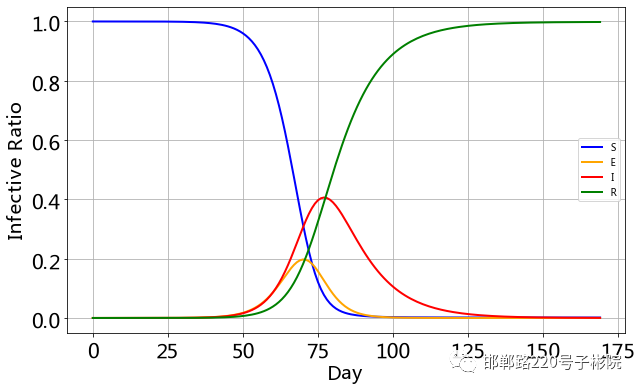 1 ~+ m$ ?. \$ x
1 ~+ m$ ?. \$ x
7 J; w( p- L2 @0 s1 w1 y
按照模型的结果,此次疫情可能真的要持续到 三四月份。这个接触率 真的非常影响表现,模型给的是个常数,但是由于政府措施的原因,这应该是个变化的值。
1 l% X0 _6 r% t+ x6 ?. }4 ]还有治愈率 也是。没有完美的模型,但是随着考虑因素的增多,就会越来越接近实际情况,从而指导政府的疫情方针政策的制定。
. X% e3 m# {+ H
+ C, U" A% ]( M! L' X/ L- |" J5 i( P) u2 q- D8 _$ x
( C3 ~0 f* m5 @8 [
7 N2 {# x4 B2 R( i
| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) |
Powered by Discuz! X2.5 |