数学建模社区-数学中国

标题: 常用模型&算法总结—图&网络模型应用—最短路径问题 [打印本页]

作者: 浅夏110 时间: 2020-5-19 14:55
标题: 常用模型&算法总结—图&网络模型应用—最短路径问题
1 两个指定顶点之间的最短路径
问题如下：给出了一个连接若干个城镇的铁路网络，在这个网络的两个指定城镇间，找一条最短铁路线。

Dijkstra算法

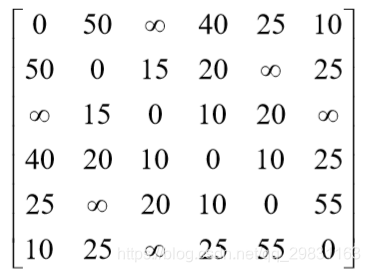
例1 某公司在六个城市中有分公司，从到的直接航程票价记在如下矩阵的位置上。（∞表示无直接航路），请帮助该公司设计一张城市到其它城市间的票价便宜的路线图。

解用矩阵（n为顶点个数）存放各边权的邻接矩阵，行向量分别用来存放P 标号信息、标号顶点顺序、标号顶点索引、短通路的值。其中分量

求第一个城市到其它城市的短路径的 Matlab 程序如下：

clc,clear
a=zeros(6);
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;
a(2,3)=15;a(2,4)=20;a(2,6)=25;
a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a';
a(find(a==0))=inf;
pb(1:length(a))=0;pb(1)=1;index1=1;index2=ones(1,length(a));
d(1:length(a))=inf;d(1)=0;temp=1;
while sum(pb)<length(a)
tb=find(pb==0);
d(tb)=min(d(tb),d(temp)+a(temp,tb));
tmpb=find(d(tb)==min(d(tb)));
temp=tb(tmpb(1));
pb(temp)=1;
index1=[index1,temp];
temp2=find(d(index1)==d(temp)-a(temp,index1));
index2(temp)=index1(temp2(1));
end
d, index1, index2

2 两个指定顶点之间最短路问题的数学表达式

例 2 最小价格管道铺设方案
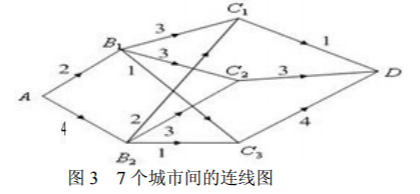
在图 3 中，用点表示城市，现有 A, B1, B2 ,C1,C2 ,C3 , D 共 7 个城市。点与点之间的连线表示城市间有道路相连。连线旁的数字表示道路的长度。现计划从城市 A 到城市 D 铺设一条天然气管道，请设计出最小价格管道铺设方案。

编写 LINGO 程序如下：

model:
sets:
cities/A,B1,B2,C1,C2,C3,D/;
roads(cities,cities)/A B1,A B2,B1 C1,B1 C2,B1 C3,B2 C1,
B2 C2,B2 C3,C1 D,C2 D,C3 D/:w,x;
endsets
data:
w=2 4 3 3 1 2 3 1 1 3 4;
enddata
n=@size(cities); !城市的个数;
min=@sum(roads:w*x);
@for(cities(i)|i #ne#1 #and# i #ne#n:
@sum(roads(i,j):x(i,j))=@sum(roads(j,i):x(j,i)));
@sum(roads(i,j)|i #eq#1:x(i,j))=1;
@sum(roads(i,j)|j #eq#n:x(i,j))=1;
end

例3 （无向图的最短路问题）

求图 4 中 v1 到 v11的最短路。分析例 2 处理的问题属于有向图的最短路问题，本例是处理无向图的最短路问题，在处理方式上与有向图的最短路问题有一些差别，这里选择赋权邻接矩阵的方法编写 LINGO 程序。

编写 LINGO 程序如下：

model:
sets:
cities/1..11/;
roads(cities,cities):w,x;
endsets
data:
w=0;
enddata
calc:
w(1,2)=2;w(1,3)=8;w(1,4)=1;
w(2,3)=6;w(2,5)=1;
w(3,4)=7;w(3,5)=5;w(3,6)=1;w(3,7)=2;
w(4,7)=9;
w(5,6)=3;w(5,8)=2;w(5,9)=9;
w(6,7)=4;w(6,9)=6;
w(7,9)=3;w(7,10)=1;
w(8,9)=7;w(8,11)=9;
w(9,10)=1;w(9,11)=2;w(10,11)=4;
@for(roads(i,j):w(i,j)=w(i,j)+w(j,i));
@for(roads(i,j):w(i,j)=@if(w(i,j) #eq# 0, 1000,w(i,j)));
endcalc
n=@size(cities); !城市的个数;
min=@sum(roads:w*x);
@for(cities(i)|i #ne#1 #and# i #ne#
n:@sum(cities(j):x(i,j))=@sum(cities(j):x(j,i)));
@sum(cities(j):x(1,j))=1;
@sum(cities(j):x(j,1))=0; !不能回到顶点1;
@sum(cities(j):x(j,n))=1;
@for(roads:@bin(x));
end

有向图相比较，在程序中只增加了一个语句@sum(cities(j):x(j,1))=0，即从顶点 1 离开后，再不能回到该顶点。

求得的最短路径为 1→2→5→6→3→7→10→9→11，最短路径长度为 13。

3 每对顶点之间的最短路径
计算赋权图中各对顶点之间最短路径，显然可以调用 Dijkstra 算法。具体方法是：每次以不同的顶点作为起点，用 Dijkstra 算法求出从该起点到其余顶点的最短路径，反复执行 n −1次这样的操作，就可得到从每一个顶点到其它顶点的最短路径。这种算法的时间复杂度为。第二种解决这一问题的方法是由 Floyd R W 提出的算法，称之为 Floyd 算法。

Floyd算法

————————————————
版权声明：本文为CSDN博主「wamg潇潇」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_29831163/article/details/89785373

作者: 德古拉 时间: 2020-5-20 08:06
good try~~

作者: 浅夏110 时间: 2020-5-21 11:37

德古拉发表于 2020-5-20 08:06
& ^5 h- G! y `- o7 V* q( vgood try~~

作者: 浅夏110 时间: 2020-5-21 11:38

德古拉发表于 2020-5-20 08:06 " _' E. f- S1 R9 k: j1 Q
good try~~

欢迎光临数学建模社区-数学中国 (http://www.madio.net/)