数学建模社区-数学中国
标题: 常用模型&算法总结—图&网络模型应用—树:连通性、最小生成树 [打印本页]
作者: 浅夏110 时间: 2020-5-21 09:56
标题: 常用模型&算法总结—图&网络模型应用—树:连通性、最小生成树
1 最大流问题的数学描述
, Z/ i$ T n: ~6 t9 Z1.1 网络中的流 定义6 I! }. W: Z5 n
在以V 为节点集, A 为弧集的有向图G = (V, A) 上定义如下的权函数:
9 s$ g' }' A' c5 u8 {" W& T8 M0 c$ R# L0 q
(i) L : A → R 为孤上的权函数,弧 (i, j)∈ A 对应的权 L(i, j) 记为 ,称为孤 (i, j) 的容量下界(lower bound);
% M6 ^8 ^8 K$ F1 e2 n' n7 ~7 {; C* n# I9 n) ^* g
(ii)U : A → R 为弧上的权函数,弧(i, j)∈ A对应的权U(i, j) 记为 ,称为孤 (i, j) 的容量上界或容量(capacity);- O+ I; e$ U! Q. o& Z# [7 X2 ?
/ K* u1 e9 U! {4 o. i6 F1 c
(iii) D :V → R 为顶点上的权函数,节点i ∈V 对应的权 D(i) 记为 ,称为顶 点i 的供需量(supply/demand);4 o3 ^( _: j+ {9 q# E; \* ]. E
?1 e ~& e8 d. D( m6 J# v
此时所构成的网络称为流网络,可以记为 N = (V, A, L,U,D) 。 由于我们只讨论V, A 为有限集合的情况,所以对于弧上的权函数 L,U 和顶点上的 权函数 D ,可以直接用所有孤上对应的权和顶点上的权组成的有限维向量表示,因此 L,U, D 有时直接称为权向量,或简称权。由于给定有向图G = (V, A) 后,我们总是可 以在它的弧集合和顶点集合上定义各种权函数,所以流网络一般也直接简称为网络。
/ @7 L% x; ? `4 T& Z& G7 E- Q- I0 O, a3 y
在流网络中,弧(i, j) 的容量下界 和容量上界表示的物理意义分别是:通过该 弧发送某种“物质”时,必须发送的最小数量为 ,而发送的最大数量为 。顶点i ∈V 对应的供需量则表示该顶点从网络外部获得的“物质”数量( > 0时),或从该顶 点发送到网络外部的“物质”数量(< 0 时)。下面我们给出严格定义。
# o+ ?: K) z* Y+ t- z
9 d; L `5 X3 f. W- e6 u5 `' @: _) [可行流(feasible flow)# { q- c9 Q$ H* I
0 H4 D6 g& I4 p. h
) M$ j3 i2 m9 G; G' F
; @; z: U% g' p; Y0 L L7 c: d* z1 m5 X! E w5 ~/ U$ X8 M
可见,当 di > 0时,表示有di 个单位的流量从网络外部流入该顶点,因此顶点i 称 为供应点(supply node)或源(source),有时也形象地称为起始点或发点等;当di < 0 时,表示有|di | 个单位的流量从该顶点流失到网络外部(或说被该顶点吸收),因此顶 点i 称为需求点(demand node)或汇(sink),有时也形象地称为终止点或收点等;当 di = 0时,顶点i 称为转运点(transshipment node)或平衡点、中间点等。此外,根据 (1)可知,对于可行网络,必有6 [9 o; U2 u6 ^! Y" P: B1 ^+ ~
: h+ D' ~& i& j3 V: E

* O4 Y6 m4 i# Q( P( M9 }) O) I0 g. {0 w9 G
也就是说,所有节点上的供需量之和为 0 是网络中存在可行流的必要条件
1 d- s. P$ n- B% D1 t" e
8 ?0 Q2 J' s4 U, w$ ?3 I V# s( u3 U
* [& k) a1 n0 L3 K X+ Q+ _ |
' b- Q9 d# S' z2 Y8 e1 ^) v& ^& Z4 n4 @0 a" \
1.2 最大流问题
. y9 V* G7 @5 s/ j5 ]% b考虑如下流网络 N = (V, A,U,D):节点 s 为网络中唯一的源点,t 为唯一的汇点, 而其它节点为转运点。如果网络中存在可行流 f ,此时称流 f 的流量(或流值,flow value)为 (根据(3),它自然也等于 − ),通常记为v 或v( f ) ,即7 u( q; `! @! g1 q+ M
7 r: c1 z6 k# X& K5 U
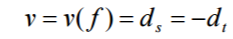 * n$ o) f* g2 e2 b$ f
* n$ o) f* g2 e2 b$ f
对这种单源单汇的网络,如果我们并不给定 和 (即流量不给定),则网络一 般记为 N = (s,t,V, A,U) 。最大流问题( maximum flow problem )就是在 N = (s,t,V, A,U) 中找到流值最大的可行流(即最大流)。我们将会看到,最大流问题 的许多算法也可以用来求解流量给定的网络中的可行流。也就是说,当我们解决了最大 流问题以后,对于在流量给定的网络中寻找可行流的问题,通常也就可以解决了。 F" p+ v, j3 Y1 }6 B3 X
* q6 h }* R' m, l! M5 x% ~用线性规划描述最大流问题
4 Y) P: w5 ~4 K* ]4 ^因此,用线性规划的方法,最大流问题可以形式地描述如下:
! P# @1 x c9 O% E' ^$ _$ s! v- E+ g% _7 p5 h4 T
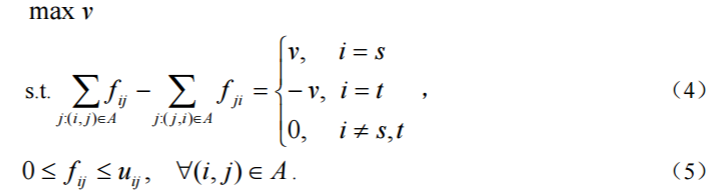
/ S) u, W* w6 [: M0 K; i# `. b0 H) E7 L
定义】 如果一个矩阵 A 的任何子方阵的行列式的值都等于0,1或 −1,则称 A 是 全幺模的(totally unimodular TU,又译为全单位模的),或称 A 是全幺模矩阵。# v( B$ s- J8 Y9 d) O6 Z
3 w/ R) G+ [! W整流定理
) ]0 U! y* u- M8 E8 ]【定理 7】(整流定理) 最大流问题所对应的约束矩阵是全幺模矩阵。若所有弧容量 均为正整数,则问题的最优解为整数解。 最大流问题是一个特殊的线性规划问题。我们将会看到利用图的特点,解决这个问 题的方法较之线性规划的一般方法要方便、直观得多。5 g5 E" L1 C% G3 {, K
& B. v9 z/ s. R8 q5 c& m& d j+ B& ^
1.3 单源和单汇运输网络4 q3 v- H: \& k5 q4 W2 M; N
多源多汇网络 转化成单源单汇网络- d7 @! q( K0 `) C) W- Q1 C
实际问题往往是多源多汇网络,为了计算的规格化,可将多源多汇网络G 化成单 源单汇网络G' 。设 X 是G 的源,Y 是G 的汇,具体转化方法如下:/ @* f( c% R: z& {0 w+ ?
2 F6 _3 ^3 P; o2 j: D/ ?: `(i)在原图G 中增加两个新的顶点 x 和 y ,令为新图G' 中之单源和单汇,则G 中 所有顶点V 成为G' 之中间顶点集。
$ a" t2 G4 u* n: G8 ]3 N x0 z2 [
; _3 l& h/ o' A/ Z. J(ii)用一条容量为∞的弧把 x 连接到 X 中的每个顶点。
9 X0 X( Z! j: e g
+ S4 p8 s D# k9 Y3 I(iii)用一条容量为∞的弧把Y 中的每个顶点连接到 y 。 G 和G' 中的流以一个简单的方式相互对应。若 f 是G 中的流,则由
z: B) j# V5 D" R" \# @8 b+ {% n4 `! T+ s' n; b& H8 X- R! }

1 P8 ~( }0 U+ }# O/ A/ o: M/ W# j; f1 L4 I8 z; S: W
2 最大流和最小割关系割的容量 ' A8 `. G% L1 I" l, \- R& {2 D' n
' A8 `. G% L1 I" l, \- R& {2 D' n
+ a& U2 O6 ^0 Q/ \. u ! ?/ D+ F* k' d9 t% f. t
! ?/ D+ F* k' d9 t% f. t
) h1 I/ u* O: i0 J) x: ~( A
则在这条可增广轨上每条前向弧的流都可以增加一个量δ ,而相应的后向弧的流可减 少δ ,这样就可使得网络的流量获得增加,同时可以使每条弧的流量不超过它的容量, 而且保持为正,也不影响其它弧的流量。总之,网络中 f 可增广轨的存在是有意义的, 因为这意味着 f 不是最大流。
; R0 x6 W7 S% s6 T+ l' P) P% o/ y) y3 A; q% \$ L" p) Q# D6 g4 O" ~
3 最大流的一种算法—标号法
- f# k. F' {- e c; `标号法是由 Ford 和 Fulkerson 在 1957 年提出的。用标号法寻求网络中最大流的基 本思想是寻找可增广轨,使网络的流量得到增加,直到最大为止。即首先给出一个初始 流,这样的流是存在的,例如零流。如果存在关于它的可增广轨,那么调整该轨上每条 弧上的流量,就可以得到新的流。对于新的流,如果仍存在可增广轨,则用同样的方法 使流的值增大,继续这个过程,直到网络中不存在关于新得到流的可增广轨为止,则该 流就是所求的最大流。
& G+ E* e$ O, a7 G2 U6 E2 w6 f7 C& j2 N, t8 A0 o! I: M9 D
这种方法分为以下两个过程:
! h4 Z) I& l0 I2 Z$ | `8 X1 l f8 ]+ h! w4 O
A.标号过程:通过标号过程寻找一条可增广轨。
+ E1 \( n, ^1 n: _: h# I& {" ]/ E8 C
B.增流过程:沿着可增广轨增加网络的流量。# f2 `& u6 y% M- Q
" S+ W3 U3 N/ e" D3 a这两个过程的步骤分述如下。
# o" U" w; t8 v5 O3 u' G3 t" O$ b3 _8 A3 k6 h
(A)标号过程:
9 W1 n% Z/ ~- r$ o, T+ S# Q' Z/ c$ b

% G8 k w' Q! x4 A$ d# \3 x- W0 j
(B)增流过程
a3 a5 \2 l4 l) K0 v/ Y! j. k* v0 G4 H# d$ C# G
网络最大流 x 的求解步骤
7 e& g$ z) G; P a1 ]. A- ~求网络 N = (s,t,V, A,U) 中的最大流 x 的算法的程序设计具体步骤如下:- E8 z. j( q6 j' }1 A1 Z
1 ^ ? O0 i2 V
对每个节点 j ,其标号包括两部分信息 (pred( j),maxf(j))0 q, \2 N( E( K: C4 d% m* y
6 j$ w/ L" B/ X& ^
该节点在可能的增广路中的前一个节点 pred( j) ,以及沿该可能的增广路到该节点为止 可以增广的最大流量 maxf( j)。
1 n* E& R( v9 F6 X7 ~7 C. L2 v5 g* c& X2 T" C/ r5 ?% e2 j
 2 }" q4 V8 I. N' f1 ]7 A+ j L3 H
2 }" q4 V8 I. N' f1 ]7 A+ j L3 H
7 s0 B" v) w0 p$ W: r
并将 j 加入 LIST 中。
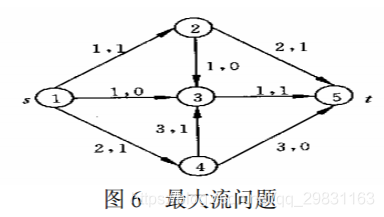
例 17 用 Ford-Fulkerson 算法计算如图 6 网络中的最大流,每条弧上的两个数字分 别表示容量和当前流量。
 o) Q W7 ^+ S4 ~0 q! ]
o) Q W7 ^+ S4 ~0 q! ]
1 `: Z: h7 q% P5 ?7 f
. V6 e2 X6 T6 V. S# ` t解 编写程序如下:. ~) f4 y# L R
. [5 U0 G4 o$ ?& v; f- \' ]
clc,clear
! {. I7 B# J' U" @3 b0 _u(1,2)=1;u(1,3)=1;u(1,4)=2;u(2,3)=1;u(2,5)=2;) ?$ p/ \7 q" E4 ^7 F9 a
u(3,5)=1;u(4,3)=3;u(4,5)=3;* x# T/ u4 o) O6 ]& Y- I. D4 N
f(1,2)=1;f(1,3)=0;f(1,4)=1;f(2,3)=0;f(2,5)=1;2 }/ |& B# u- _
f(3,5)=1;f(4,3)=1;f(4,5)=0;1 \5 [( q$ S, t2 {6 I
n=length(u);list=[];maxf(n)=1;2 a$ X5 N& x5 X6 o4 t6 T- m, [
while maxf(n)>0
0 p! b1 P* v) x8 W) L; w: Rmaxf=zeros(1,n);pred=zeros(1,n);8 x" i; b! `: `5 h7 W9 `
list=1;record=list;maxf(1)=inf;% \' U- ]7 j' a4 A5 ?
% list是未检查邻接点的标号点,record是已标号点 B8 A, k$ e0 x K; J- X0 v
while (~isempty(list))&(maxf(n)==0)9 w! d9 C" D* @! \& S/ W
flag=list(1);list(1)=[];* ]( a. N9 f; r( f( ]- ]1 e6 e$ M
label1= find(u(flag, -f(flag,
-f(flag, );
);
2 y* D3 X& t9 E G8 O( f label1=setdiff(label1,record);
" x7 q) l8 e M4 A/ B list=union(list,label1);
/ Q8 U0 l. I4 K& Z8 D pred(label1)=flag;
" B! X/ A) T* q% T maxf(label1)=min(maxf(flag),u(flag,label1)...
( E8 E# i6 b# W8 X7 `8 n- \5 `! f3 \ -f(flag,label1));9 j# i2 P9 V' x8 b, c
record=union(record,label1);0 a4 k& @/ ?" d2 ^8 `( _) M
label2=find(f(:,flag));0 Q! l0 Q- K# P7 ]$ H$ F k* Z
label2=label2';
+ Q0 u( i! F5 w% [6 G& f label2=setdiff(label2,record);& g+ _# {. A1 w& o
list=union(list,label2);6 z0 d' a, {) o3 d( h
pred(label2)=-flag;
& w( @* p9 S+ E p2 A4 y# Y( D maxf(label2)=min(maxf(flag),f(label2,flag));" ^9 K4 t* B& w! d; p& v3 `
record=union(record,label2);
G+ Z" s! x* M4 z0 s7 x end
0 d# b. A6 W3 Z$ O* i. g6 @ if maxf(n)>0
) r( z7 e& D0 T8 y% ?) n v2=n; v1=pred(v2);
# \( z# i' w: w, d- C while v2~=1
6 I4 C' [ a1 P, T/ U6 E if v1>0
" \+ y1 ^$ T& l3 M9 l% j f(v1,v2)=f(v1,v2)+maxf(n);
* |4 i$ `; W/ Z) I else
* t, R! J2 y% H v1=abs(v1);" d+ J" D Q5 P5 ^$ T/ c: w
f(v2,v1)=f(v2,v1)-maxf(n);
' f* ^# ]& _' u: K/ w" u end
+ W2 d5 R8 D: Q& j: ~ v2=v1; v1=pred(v2);' S. @% [6 v, _0 |3 n, ~2 s9 ?0 Y
end
- i/ a% F6 o- M* l% k3 v8 z* s end+ r L( ` m' ] ]% \- m, L
end
# y Q2 s* Z4 p, p. J' w$ Sf
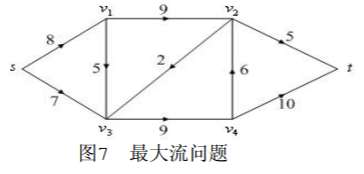
1 l2 I7 N3 Y: O; m: ^例18 现需要将城市 s 的石油通过管道运送到城市t ,中间有4个中转站 v1 ,v2 ,v3 和 v4 ,城市与中转站的连接以及管道的容量如图7所示,求从城市 s 到城市t 的最大流。
6 H. g5 K7 M1 ~" S* [7 t$ ^- f) l
+ s( |, R W. f1 T( N4 _8 L' z, M) v- _1 b
: b( F7 w4 E- d# n" B* g2 X; D
0 e1 I G8 P% C: S4 {! T& r解 使用最大流的数学规划表达式,编写LINGO程序如下:- h* d! F# v" C3 c, F
8 r7 E c/ y) O) `
model:
l7 A2 |! B" osets:
/ g. E+ K" G3 V5 L anodes/s,1,2,3,4,t/;, u' h( \0 I' ?1 }
arcs(nodes,nodes)/s 1,s 3,1 2,1 3,2 3,2 t,3 4,4 2,4 t/:c,f;; o+ {; W9 Z) c8 H$ ^: n. W, z) G
endsets
& e) K" p7 M) o2 Rdata:
3 l$ v' c/ [( b$ mc=8 7 9 5 2 5 9 6 10;
7 k; e/ C2 g& l5 L( L/ s* ?" U' _enddata# F( V4 d; i( \2 K# |
n=@size(nodes); !顶点的个数;
5 w$ z4 ]: W$ F, W Omax=flow;' ?5 w, @6 f" m M
@for(nodes(i)|i #ne#1 #and# i #ne# n:0 [# ] g6 z" d' x7 e# g- d
@sum(arcs(i,j):f(i,j))=@sum(arcs(j,i):f(j,i)7 f2 w$ P/ n9 z1 {7 A7 R$ d
@sum(arcs(i,j)|i #eq# 1:f(i,j))=flow;2 [# x5 d+ @' P3 U7 J$ u. I ^; {
@sum(arcs(i,j)|j #eq# n:f(i,j))=flow;( b3 V) \$ a0 i1 A$ P$ T
@for(arcs bnd(0,f,c));
bnd(0,f,c));
# m7 h# y* r% M7 V$ Jend
" L# C9 S/ l+ \" t0 u
+ n! y* z% k% a8 F在上面的程序中,采用了稀疏集的编写方法。下面介绍的程序编写方法是利用赋权邻 接矩阵,这样可以不使用稀疏集的编写方法,更便于推广到复杂网络。. z3 G- L+ N) t3 W
4 H5 P! Q# s M8 A
model:; N$ g! g; R! f
sets:
4 b, O! ?" n$ enodes/s,1,2,3,4,t/;" l% Y" w. j! o- r( R
arcs(nodes,nodes):c,f;" y2 w6 y( _( W$ x1 x; \
endsets4 ^# p4 }1 A- `
data:: v4 |9 t4 e; i2 f
c=0;& e/ ?. v* G! @! W8 v* d& h/ ^
@text('fdata.txt')=f;7 m* _$ L! Q8 M. S1 c8 K
enddata
9 S: Y8 `; u* n. Q2 [ mcalc:
* d+ p! H0 o( y- w2 Lc(1,2)=8;c(1,4)=7;
* d$ H0 Z, L, Q) k; @$ @) jc(2,3)=9;c(2,4)=5;( n. k8 z" h3 P
c(3,4)=2;c(3,6)=5;
m% d) `+ p3 N* xc(4,5)=9;c(5,3)=6;c(5,6)=10;
$ k9 R/ T# u: b T" n$ q$ P! nendcalc
9 z( r( O6 O9 U: A0 t8 L/ j/ An=@size(nodes); !顶点的个数;* } E) s( T/ E) `' N5 U, F8 d, O2 @3 v# X
max=flow;
' j" Y3 |* B$ c) Z7 m4 n@for(nodes(i)|i #ne#1 #and# i #ne# n:5 u7 Z9 p7 h1 j7 X
@sum(nodes(j):f(i,j))=@sum(nodes(j):f(j,i)));
6 v! P( t* D" _( j. Q@sum(nodes(i):f(1,i))=flow;, G) `4 K e2 q9 o, g% ~" g1 i
@sum(nodes(i):f(i,n))=flow;
' P' S& k8 ]5 Z. q& z@for(arcs bnd(0,f,c));
bnd(0,f,c));
3 k% i! I- |+ ^end
v+ f- v- y& S( |3 x) |! g* m0 V
9 t% ]" j6 n6 q" C# u————————————————( y/ ^# Q0 n3 S$ z( O
版权声明:本文为CSDN博主「wamg潇潇」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
) Y) N2 ]% d5 V+ d8 v9 j, [原文链接:https://blog.csdn.net/qq_29831163/article/details/89786313$ j) |6 f! ~2 j
- | [% p3 l1 X* x3 V
, Y/ H. M% _1 j7 g2 O; h& J
| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) |
Powered by Discuz! X2.5 |




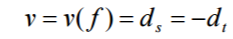 * n$ o) f* g2 e2 b$ f
* n$ o) f* g2 e2 b$ f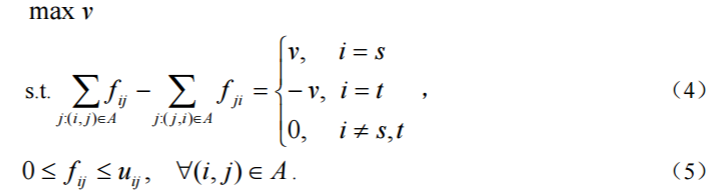

 ' A8 `. G% L1 I" l, \- R& {2 D' n
' A8 `. G% L1 I" l, \- R& {2 D' n ! ?/ D+ F* k' d9 t% f. t
! ?/ D+ F* k' d9 t% f. t

 2 }" q4 V8 I. N' f1 ]7 A+ j L3 H
2 }" q4 V8 I. N' f1 ]7 A+ j L3 H o) Q W7 ^+ S4 ~0 q! ]
o) Q W7 ^+ S4 ~0 q! ] -f(flag,
-f(flag, );
);
 bnd(0,f,c));
bnd(0,f,c)); bnd(0,f,c));
bnd(0,f,c));