数学建模社区-数学中国
标题: 组合优化算法-现代优化算法(三):禁忌搜索算法 [打印本页]
作者: 浅夏110 时间: 2020-5-22 15:25
标题: 组合优化算法-现代优化算法(三):禁忌搜索算法
1 禁忌搜索算法的相关概念
- t8 K( t+ b( _: U# o4 ^6 R& A禁忌搜索算法是组合优化算法的一种,是局部搜索算法的扩展。禁忌搜索算法是人 工智能在组合优化算法中的一个成功应用。禁忌搜索算法的特点是采用了禁忌技术。所 谓禁忌就是禁止重复前面的工作。禁忌搜索算法用一个禁忌表记录下已经到达过的局部最优点,在下一次搜索中,利用禁忌表中的信息不再或有选择地搜索这些点。 禁忌搜索算法实现的技术问题是算法的关键。禁忌搜索算法涉及侯选集合、禁忌 对象、评价函数、特赦规则、记忆频率信息等概念。5 E9 s/ p/ u6 h7 S* h7 p
1 \$ v4 q# Y3 B# o+ b% y
(1)邻域
% {" J" T2 v: T7 e" S+ j在组合优化中,距离的概念通常不再适用,但是在一点附近搜索另一个下降的点仍 然是组合优化数值求解的基本思想。因此,需要重新定义邻域的概念。* S% {- ~3 ~$ t- e! X c5 _# J x
# G3 b" O( u" r4 q p5 N
 1 M' _7 V, A7 q: T" n; S$ T7 B0 p
1 M' _7 V, A7 q: T" n; S$ T7 B0 p
/ g, u/ g! H1 l/ x' v: H
# U- g% p) y2 _! t# Q+ _(2)侯选集合
. l! u- d5 P( I2 Y侯选集合由邻域中的邻居组成。常规的方法是从邻域中选择若干个目标值或评价 值最佳的邻居入选。
6 J/ b7 u+ [6 {$ V8 T) O& b/ z. F$ N4 g8 T1 E3 m. ?
(3)禁忌对象和禁忌长度4 x: E; f8 [2 n* F& [8 W* d8 N
禁忌表中的两个主要指标是禁忌对象和禁忌长度。禁忌算法中,由于我们要避免 一些操作的重复进行,就要将一些元素放到禁忌表中以禁止对这些元素进行操作,这些元素就是我们指的禁忌对象。禁忌长度是被禁对象不允许选取的迭代次数。一般是给被禁对象 x 一个数(禁忌长度) t ,要求对象 x 在 t 步迭代内被禁,在禁忌表中采用 tabu(x) = t 记忆,每迭代一步,该项指标做运算 tabu(x) = t −1,直到 tabu(x) = 0时 解禁。于是,我们可将所有元素分成两类,被禁元素和自由元素。禁忌长度t 的选取可以有多种方法,例如t = 常数,或t = [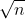 ],其中 n 为邻域中邻居的个数;这种规则容易在算法中实现。
],其中 n 为邻域中邻居的个数;这种规则容易在算法中实现。
j4 G9 A; z+ v: x. ^- `( Y" [0 l9 x, a
(4)评价函数1 u# M8 @6 |2 b" g" X
评价函数是侯选集合元素选取的一个评价公式,侯选集合的元素通过评价函数值 来选取。以目标函数作为评价函数是比较容易理解的。目标值是一个非常直观的指标, 但有时为了方便或易于计算,会采用其他函数来取代目标函数。
2 K9 A' r& }+ x1 S+ ~2 r G+ x+ D, `
(5)特赦规则: k3 q- W/ J' d
在禁忌搜索算法的迭代过程中,会出现侯选集中的全部对象都被禁忌,或有一对 象被禁,但若解禁则其目标值将有非常大的下降情况。在这样的情况下,为了达到全局 最优,我们会让一些禁忌对象重新可选。这种方法称为特赦,相应的规则称为特赦规则。
+ `8 h+ B2 S+ W0 V: V8 k8 C" x
9 |+ h8 r4 X7 ^1 ^. |) @(6)记忆频率信息) I! V1 \" E ?
在计算的过程中,记忆一些信息对解决问题是有利的。如一个最好的目标值出现 的频率很高,这使我们有理由推测:现有参数的算法可能无法再得到更好的解。根据解 决问题的需要,我们可以记忆解集合、被禁对象组、目标值集合等的出现频率。 频率信息有助于进一步加强禁忌搜索的效率。我们可以根据频率信息动态控制禁 忌的长度。一个最佳的目标值出现的频率很高,有理由终止计算而将此值认为是最优值。7 w% W1 c. R5 f% c- a: b r, h
. E+ ]) J b8 Y0 k' ]4 F* S2 模型及求解5 \: \# S7 W7 n4 e
我们用禁忌搜索算法研究如下的两个问题:' o; @4 L& O. E5 L
1 J0 D8 U; [7 ]+ k9 t(1)研究 1.2 中同样的问题。. X% q9 C' u3 a& X: I- \6 u
' V' t% S( u5 c! ^' w% g3 P
/ B U8 a) l, b: q& D3 q8 t0 l& |% y
$ |( }! g+ K7 s/ s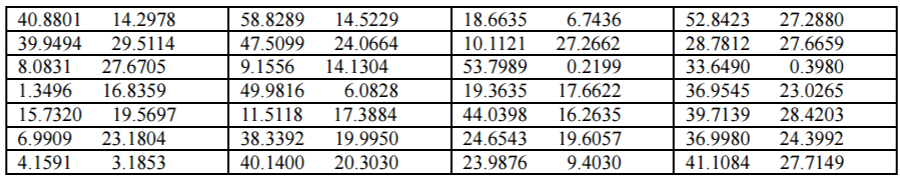
( ^2 U$ n( e, u9 H2 A$ I( h3 E% ?/ S- o) |5 s3 t: l
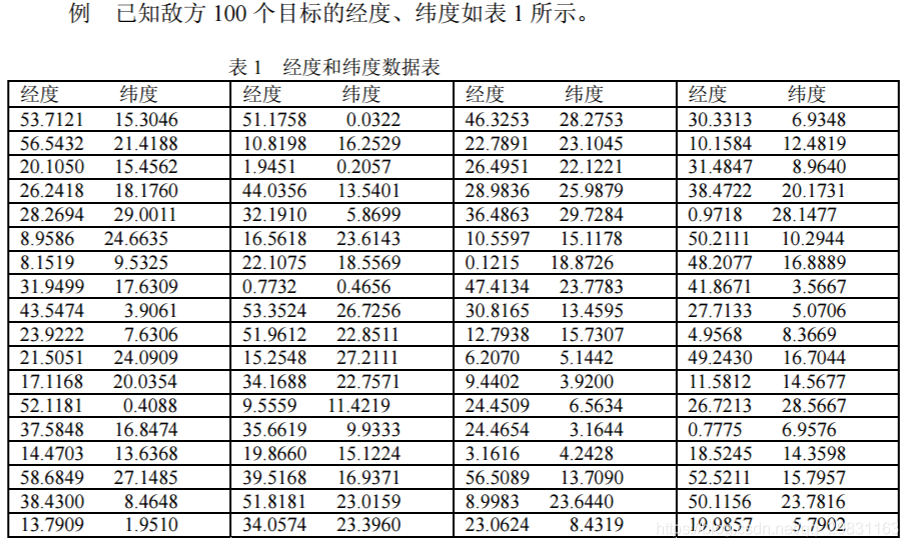
我方有一个基地,经度和纬度为(70,40)。假设我方飞机的速度为 1000 公里/小时。 我方派一架飞机从基地出发,侦察完敌方所有目标,再返回原来的基地。在敌方每一目 标点的侦察时间不计,求该架飞机所花费的时间(假设我方飞机巡航时间可以充分长)。
0 l* w* [8 u' b0 ]- z5 A! a" F3 w. T! @+ F9 _: @

. {% k2 S: p# ~6 J. p5 Q& t! c' Q3 ~0 i
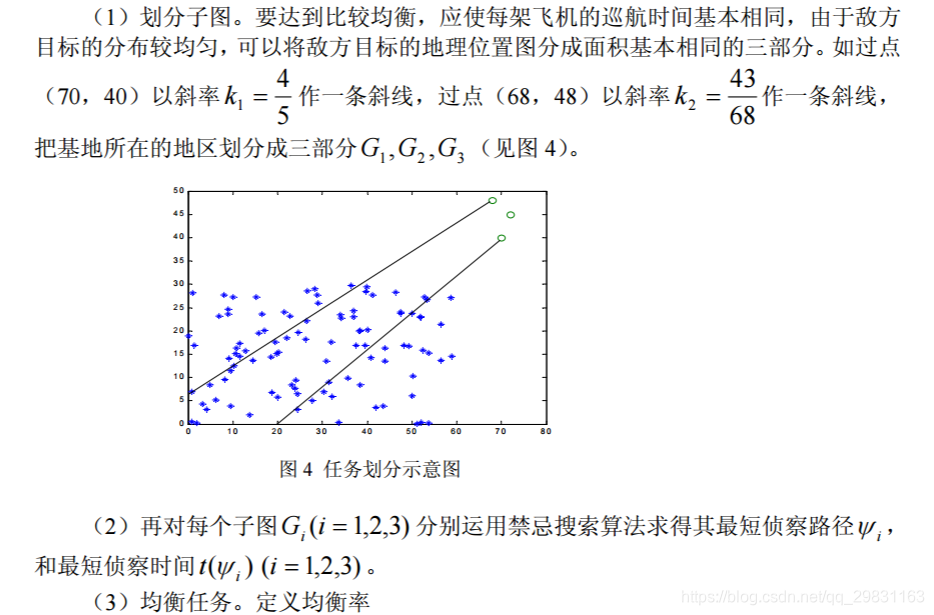
(2)我方有三个基地,经度、纬度分别为(70,40),(72,45),(68,48)。假设我方 所有无人侦察机的速度都为 1000 公里/小时。三个基地各派出一架飞机侦察敌方目标, 怎样划分任务,才能使时间最短,且任务比较均衡。6 O" _' P. T* K9 X3 c; \
) W! @9 s; w1 _$ [( ~' A. a
2.1 问题(1)的求解
! t$ d) f& `* [* Z. D$ ~! f/ L求解的禁忌搜索算法描述如下: (1)解空间
! b. B% A/ {3 ~& q: W$ W0 p; A! A( C6 d* N+ F# E$ R" y

. o" g' k4 a/ P! \1 u& b
: [/ y% f0 B3 c3 K) `/ X: J(2)目标函数
目标函数为侦察所有目标的路径长度。我们要求
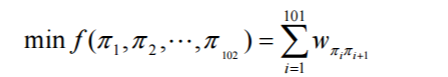 2 h. n4 p" a" U/ o3 Q5 |. I
2 h. n4 p" a" U/ o3 Q5 |. I
6 P8 p' X4 O1 R a; e3 [
(3)候选集合' H! X+ E, q% g; a ^2 {* H
3 Q2 p" u( d! ?( k: f) r
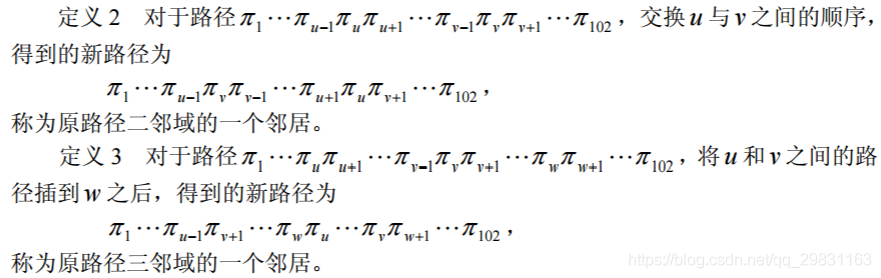 ; [/ g% u4 m) D3 [; |& f
; [/ g% u4 m) D3 [; |& f
: J+ G! ^& g H5 x ?
如果要考虑当前解的全部二邻域(或三邻域)的邻居,将面临着太大的工作量。 因此我们用随机选取的方法每次选取50个邻居组成的集合作为侯选集合。而将省下的 时间作更多次搜索,这样做同样可以保证较高的精确度,同时可以大大提高算法的效率。
(4)禁忌长度及禁忌对象
" ?/ A& R: N; \9 P, K# ^( {

2 j; I3 }- t! N6 c$ `$ k6 O& n1 E9 N) r" b
我们把禁忌表设计成一个循环队列,初始化禁忌表 H = Φ 。从候选集合C 中选出 一个向量 x ,如果 x ∉ H ,并且 H 不满,则把向量 x 添加到禁忌表中;如果 H 已满, 则最早进入禁忌表的向量出列,向量 x 进入到出列的位置。3 d( k* `/ _5 V4 j9 z
, d% Y- _: @) ^4 ?; |" |
(5)评价函数
8 Q) T1 O F, H5 j1 Z
1 p) O% j$ n& w! g可以用目标函数作为评价函数,但是这样每选取一个新的路径都得去计算总时间, 计算量比较大。对于上述二邻域中的邻居作为侯选集合,每一个新路径中只有两条边发 生了变化,因此将目标函数的差值作为评价函数可以极大地提高算法的效率。评价函数 取为1 l" s% N1 \. O
1 \3 m% W5 f# V1 G" c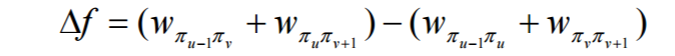 . j: i+ @$ d; B- v2 W
. j: i+ @$ d; B- v2 W
; ^+ r' t4 O$ `# e0 `
禁忌搜索算法的流程禁忌搜索算法的流程如下:
' J1 u* N' z" b- k! V5 i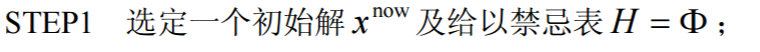 5 c+ v! B, W5 Z' O, L1 ?1 e
5 c+ v! B, W5 Z' O, L1 ?1 e
% {& _/ W" n& s* }$ P
4 p6 Y5 T2 Q1 B4 k- l
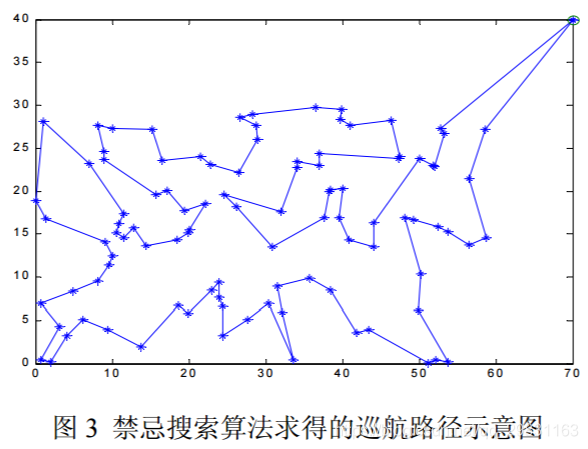
# r" p5 N5 E! Z3 u利用 Matlab 程序求得,我们的巡航时间大约在 41 小时左右,其中的一个巡航路径 如下图所示
* D# y9 L4 p: _) `" e( c% E4 r; n) C6 [ e; X& ^
4 J. u1 i$ k9 C/ x4 w3 u0 o) U3 h0 W# W2 m6 a4 l
2.2 问题(2)的求解对于这个问题,我们的基本想法是,先根据敌方基地的分布特点将敌方的基地大体 划分在三个区域之内,并使三架侦察机分别对这三个区域的敌军基地进行侦察,求取各 自的最短时间。然后对任务不均衡区域之中的点做适当调整。 我们解决问题的步骤如下:
 4 H- F( P$ y# H; i
4 H- F( P$ y# H; i
0 V3 \1 Q+ {, C! m1 c7 M r6 J 5 \% w6 q$ E- P% J1 C' B- y) q
5 \% w6 q$ E- P% J1 C' B- y) q
/ T9 s. b! T6 S1 Z4 O* ^. E! p————————————————; p: x+ q; ?1 K8 B% P" D
版权声明:本文为CSDN博主「wamg潇潇」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。& m9 V. b6 B! r5 H. \! Q. \
原文链接:https://blog.csdn.net/qq_29831163/article/details/89670768$ c P9 T( T$ f* j
5 X+ F% l6 f* Y! p$ F7 }: u9 I' R
| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) |
Powered by Discuz! X2.5 |
 1 M' _7 V, A7 q: T" n; S$ T7 B0 p
1 M' _7 V, A7 q: T" n; S$ T7 B0 p



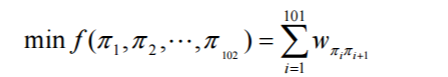 2 h. n4 p" a" U/ o3 Q5 |. I
2 h. n4 p" a" U/ o3 Q5 |. I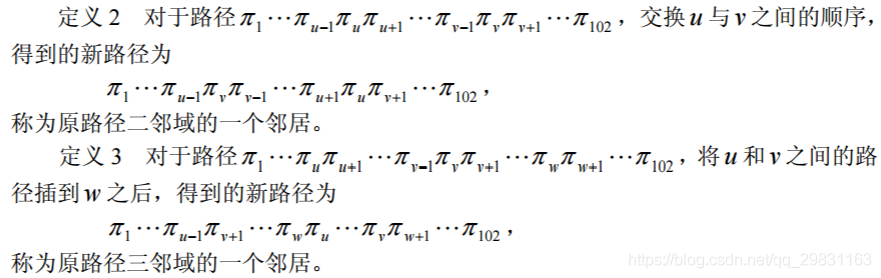 ; [/ g% u4 m) D3 [; |& f
; [/ g% u4 m) D3 [; |& f
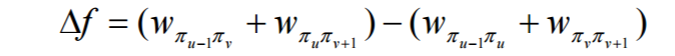 . j: i+ @$ d; B- v2 W
. j: i+ @$ d; B- v2 W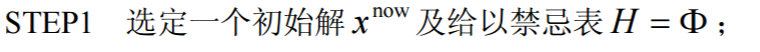 5 c+ v! B, W5 Z' O, L1 ?1 e
5 c+ v! B, W5 Z' O, L1 ?1 e

 4 H- F( P$ y# H; i
4 H- F( P$ y# H; i 5 \% w6 q$ E- P% J1 C' B- y) q
5 \% w6 q$ E- P% J1 C' B- y) q