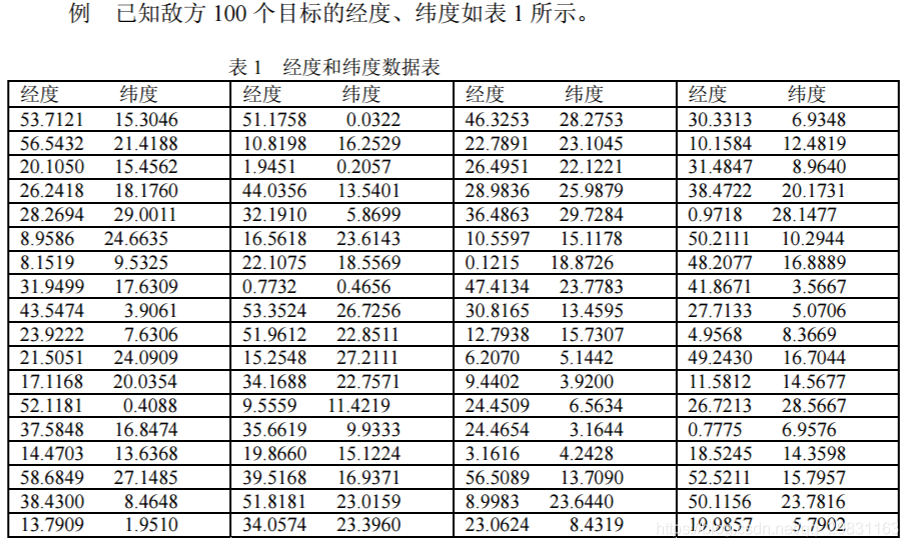
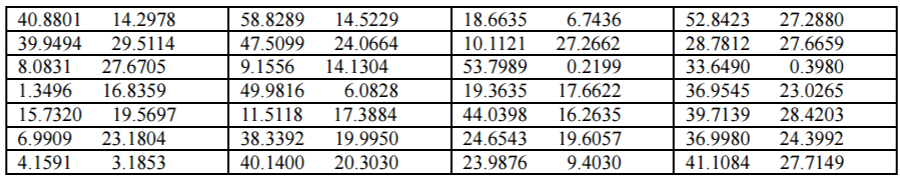
 ( I; W# m; W# M/ y# a
( I; W# m; W# M/ y# a 0 A( ^3 _8 l! S! r5 ^7 q
0 A( ^3 _8 l! S! r5 ^7 q
 $ _5 q" A, Z3 a/ E) o3 b, x
$ _5 q" A, Z3 a/ E) o3 b, x ;
; ;
; -3+ t; {6 S- Q, n% X
-3+ t; {6 S- Q, n% X -1
-1 ;& }# r: a" `% p) ?5 t
;& }# r: a" `% p) ?5 t 35 j8 X& e1 C( \% w
35 j8 X& e1 C( \% w =C(j,[1:bw(1)-1,bw(2)+1:bw(3),bw(1):bw(2),bw(3)+1:102]); * l' {6 R% P" o" f, ^" ?
=C(j,[1:bw(1)-1,bw(2)+1:bw(3),bw(1):bw(2),bw(3)+1:102]); * l' {6 R% P" o" f, ^" ? ;
;
 ' Q/ ^7 j; [# O- M
' Q/ ^7 j; [# O- M| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) | Powered by Discuz! X2.5 |