
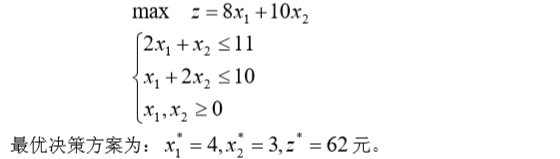 2 l6 t. ? o% k" @ F+ {
2 l6 t. ? o% k" @ F+ { + G# w1 u# i" `# W# z9 U3 x1 Y
+ G# w1 u# i" `# W# z9 U3 x1 Y 7 [; _* @1 `! N! Q0 q- M
7 [; _* @1 `! N! Q0 q- M
 1 T5 C/ S# P6 T# r4 v2 K
1 T5 C/ S# P6 T# r4 v2 K
 3 z0 T: F0 E0 R6 _2 N _+ g/ d$ ]3 J
3 z0 T: F0 E0 R6 _2 N _+ g/ d$ ]3 J : C2 o3 {5 {5 t }$ [
: C2 o3 {5 {5 t }$ [
 : I% r2 J B$ J% \# k$ D; n7 u
: I% r2 J B$ J% \# k$ D; n7 u
 sum(Variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i));
sum(Variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i)); 求得 dminus(1)=0,即目标函数的最优值为 0,第一级偏差为 0。
求第二级目标,LINGO 程序如下:
model: sum(Variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i)); ( N" t; d# `7 X6 X Z
sum(Variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i)); ( N" t; d# `7 X6 X Z gin(x)); 3 j5 i2 ?- A) X, w0 n! b& L$ b9 Z
gin(x)); 3 j5 i2 ?- A) X, w0 n! b& L$ b9 Z sum(Variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i));
sum(Variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i));  sum(variable(j):a(i,j)*x(j))<b(i)); @for(s_con_num(i)
sum(variable(j):a(i,j)*x(j))<b(i)); @for(s_con_num(i) sum(variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i)); @for(level(i)|i #lt# @size(level)
sum(variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i)); @for(level(i)|i #lt# @size(level) bnd(0,z(i),goal(i)));
bnd(0,z(i),goal(i)));  4 m6 R6 S7 Y3 \9 n
4 m6 R6 S7 Y3 \9 n多目标规划可以归结为
/ R8 R( Q5 [. {% M

就可求得问题的解。
习题' p U' ~" n* p% s2 X
| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) | Powered by Discuz! X2.5 |