

解 建立目标约束。
(1)装配线正常生产

(2)销售目标

(3)加班限制

写出目标规划的数学模型

写出相应的LINGO程序如下:
model: $ m. d: z& F' A! y' ` sum(variable(j):c(i,j)*x(j))+dminus(i)-dplus(i)=g(i));
sum(variable(j):c(i,j)*x(j))+dminus(i)-dplus(i)=g(i));  bnd(0,z(i),goal));
bnd(0,z(i),goal)); 
 ( e, P" w1 h) U J5 _
( e, P" w1 h) U J5 _

 , k, A: Y6 I6 F. k4 D6 Y: t
, k, A: Y6 I6 F. k4 D6 Y: t sum(customer(j):x(i,j))<a(i)); x(3,1)+dminus(1)-dplus(1)=100;
sum(customer(j):x(i,j))<a(i)); x(3,1)+dminus(1)-dplus(1)=100;  sum(plant(i):x(i,j))+dminus(1+j)-dplus(1+j)=0.8 *b(j);
sum(plant(i):x(i,j))+dminus(1+j)-dplus(1+j)=0.8 *b(j);  bnd(0,z(i),goal));
bnd(0,z(i),goal)); 
 ( V f7 {/ l3 @% k
( V f7 {/ l3 @% k
 o m" j/ x" U W% f
o m" j/ x" U W% f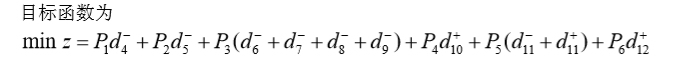 \. a( H* w4 A& q8 g1 b. n3 i
\. a( H* w4 A& q8 g1 b. n3 i
 ! ~9 T9 T( D8 m
! ~9 T9 T( D8 m $ U& z- o) q, q
$ U& z- o) q, q & z7 B, O8 ^" Z, v9 t0 y' f
& z7 B, O8 ^" Z, v9 t0 y' f
 9 ^: o) Z, ^6 {! U9 h$ S
9 ^: o) Z, ^6 {! U9 h$ S
| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) | Powered by Discuz! X2.5 |