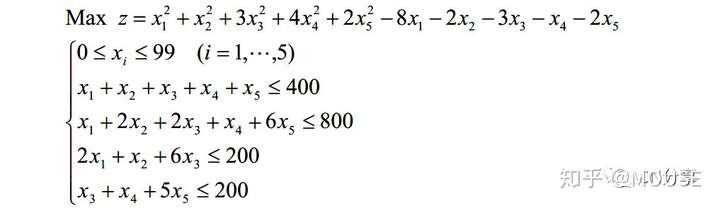数学建模社区-数学中国
标题: 助力国赛 | 第3弹 规划问题(Lingo版) [打印本页]
作者: 杨利霞 时间: 2020-6-7 14:34
标题: 助力国赛 | 第3弹 规划问题(Lingo版)
m, e0 M% X& I+ Y7 G
助力国赛 | 第3弹 规划问题(Lingo版)& a5 K" r; I5 f) H5 a( I
$ {* W( b. M1 Q, ], d- q
1 k5 g9 G- ]2 M" \8 {前言上次介绍了用MATLAB来求解规划问题,功能强大是强大,但总觉得有点不爽,函数里面的参数有点难记,万一输错了岂不玩完了。的确在可读性这方面,MATLAB做的差一点。正是基于此在此向各位推荐另一款软件——Lingo。Lingo在数学规划上也是大名鼎鼎的。本次首先会简单介绍下Lingo和其基本操作,齐次介绍些高级操作,最后还是回到实际问题中,在具体问题中一睹Lingo的强大。
- 基本操作
- 高级操作
- 实际应用# x% i9 W" x# U5 O' l
# x! [, A; y6 M4 w2 a/ H基本操作简介Lingo是美国Lindo系统公司开发的一套专业的求解最优化问题的软件包,可以求解线性规划、二次规划、非线性规划、线性方程组、非线性方程组和整数规划等。LINGO软件有多种版本,如LINDO,GINO 和LINGO(包括LINGO NL)软件。在这些软件中关系最让人“头痛”的恐怕就时Lingo与Lindo的关系,其实可以这样简单的理解:Lindo是可以是这些软件集合的代名词,Lingo只是其中一种具体的软件而已。管他们什么关系,知道现在被广泛使用的是Lingo就行了。: y5 x k- B) s& G2 q
Lingo是一款商业软件,使用是需要付费的,可以登录他们的官网:http://www.lindo.com 进行查看,但在天国获取的方法就不仅限于此了,具体可以访问某度,在此就不细说了。7 \0 k1 E- @0 [" ?3 y
; {9 } ?$ V( K! B- E: d下面“吹一吹”Lingo。
强大的求解整数规划功能是Lingo软件的最大特色,且求解速度非常快。Lingo还是最优化问题的一种数学建模语言,它包括许多常用的数学函数,这些函数可供使用者在建立最优化模型时调用。此外,Lingo提供与文本文件、Excel文件和数据库文件的接口,便于输入、求解和分析大规模最优化问题。
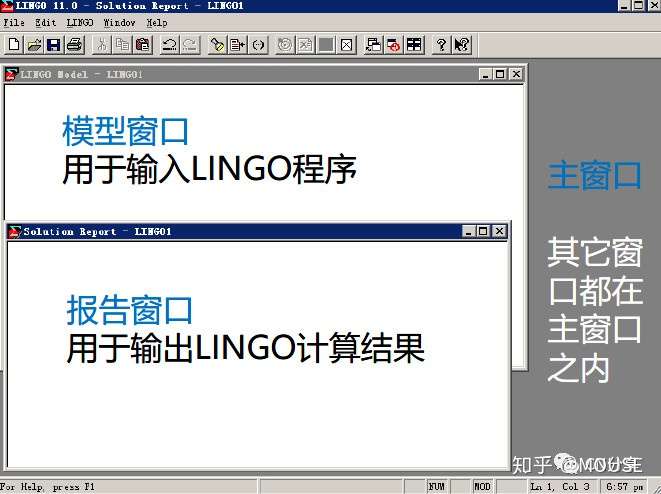
2 I8 T" C2 J& W7 @, Q! d0 ^8 f! R初印象第一眼还是很重要的,下面就看一看Lingo。; e+ O v5 k, [
建面如下:9 \) u; I* C# _1 h' w" ]4 z. i
 : Z* J0 d. X! L1 T# Y
: Z* J0 d. X! L1 T# Y
常用工具栏:
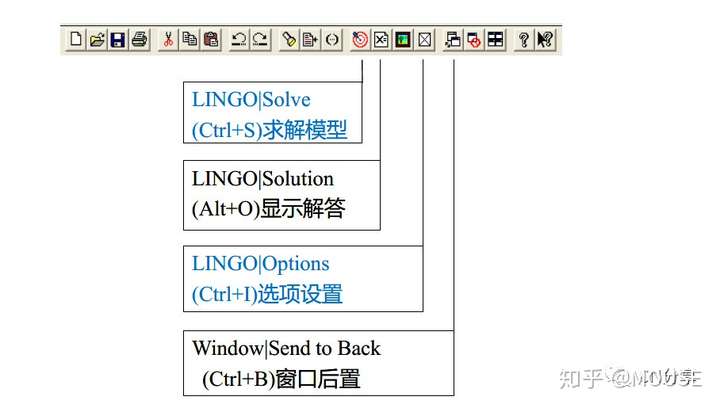
) y2 x; {8 J( }: n+ C o( pLingo文件类型:
文件后缀名为“.lg4”保存了模型窗口中所能够看到的所有文本和其他对象及其格式信息。
 运算符
运算符算数运算符: 用于数与数之间的数学运算。& v' @: p( O' q9 t( x1 [
LINGO中的算术运算符有以下5种:, Q* A6 K7 ~0 J
+(加法)$ Z) F. J7 j+ }" d
-(减法或负号)
$ C% d0 p- M. A9 I- o*(乘法), f/ Y- d) T2 q7 o6 ^
/(除法)
; j# m; w$ i0 v$ Y2 P4 K, ]^ (求幂)
关系运算符:表示“数与数之间”的大小关系。
/ e' F4 Q$ z4 o. yLINGO中关系运算符有3种:, Q/ O$ E& F, ~- `0 e
< (即<=,小于等于)" U. C& |( q, ?+ Q
= (等于)
7 T( A5 c7 @4 }/ P: ^> (即>=,大于等于)
简单程序编写求解如下问题:
7 ]# y0 A3 Q* e3 N/ z7 w; [
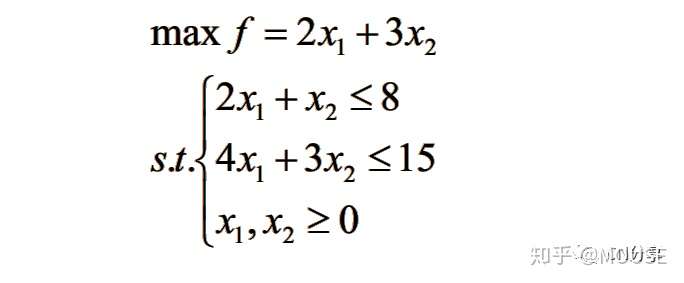
/ c+ d1 C P- a编写程序:
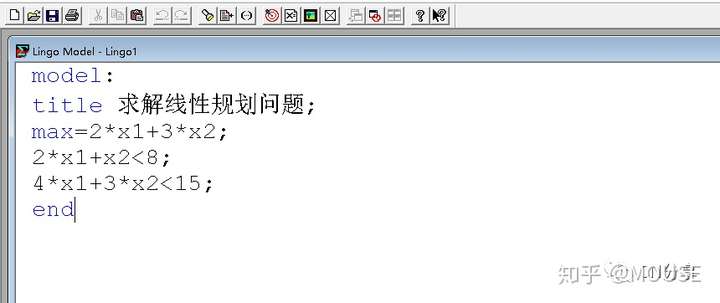
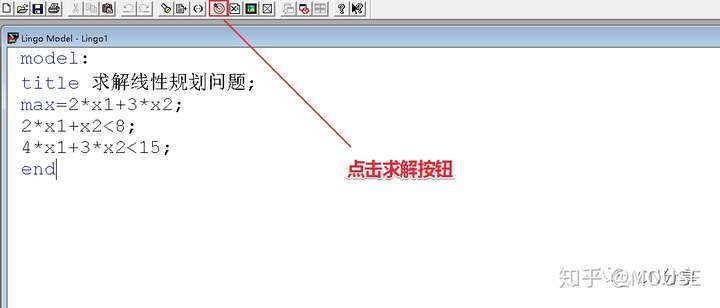
* n# P- a; }6 y0 ~: X点击求解按钮:
 1 \, C( }& |( K6 N5 D/ ^& t% t, D5 U
1 \, C( }& |( K6 N5 D/ ^& t% t, D5 U
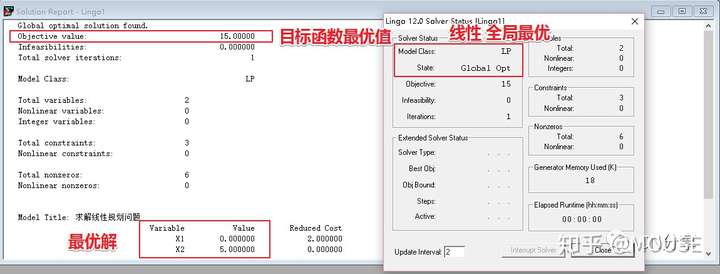
分析结果:
 ) p. a9 L, ~( n( t! f
) p. a9 L, ~( n( t! f
所以当x1 = 0,x2 = 5时,取得目标函数的最优值15。
高级操作下面详细介绍Lingo的用法。
基本语法在LINGO语句中通常以MODEL开始,END结束(MODEL和END行也可以删除),目标函数表达式前需要加“MAX=”或“MIN=”. 在写LINGO模型中,注意:
- LINGO模型已假设各个决策变量非负. 若变量无非负约束或有上下界,则可以考虑用@free、@sub、@slb或@bnd来定义.
- 变量名不能超过32个字符,且必须以字母(A-Z)开头,其后可以是字母、数字(0-9)和下划线(_)的任意组合.
- 变量名不区分大小写.
- 在约束中“>=”与“>”等同,“<=”与“<”等同.
- 在目标函数或约束条件中需要以“;”结束.
- 标点符号等要在英文状态下输入.
- “!”为注释符号,其后为注释内容,注释以“;”结束.
- 逻辑运算主要包括:#EQ#(等于),#NE#(不等于),#GE#(大于等于),#LT#(小于),#LE#(小于等于)." a* \2 F0 l/ o* p6 y0 @ I# {+ M0 X
段LINGO中建立的优化模型可以由六个部分组成,或称为六“段”。
- 集合段:用于定义数组型性变量SETS: ……ENDSETS
- 数据段:用于变量赋值与数据传递DATA: ……ENDDATA
- 目标与约束段:用于列出目标与约束唯一一个没有段的开始和结束标记
- 计算段:用于数据初始整理计算CALC: ……ENDCALC
- 初始段:用于变量赋初值迭代寻优INIT: ……ENDINIT
- 子模型段:用于表达子模型进行调用@SUBMODEL mymodel:可执行语句(约束+目标)ENDSUBMODEL) q7 W% Y% I! |9 h
有了这些我们就可以,不必把表达式全都列举出来了,下面这个表达方式:4 g) ]2 x5 X2 L! d0 {4 k
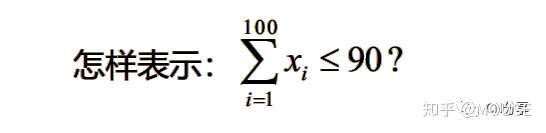
* O% x3 L6 b: Q+ {$ }. icode:
sets:!集合段;s/1..100/:x;!基本集合, 集合名与属性变量;endsets!目标与约束段;@sum(s(i):x(i))<90;!循环求和函数;1 h, ?. ~: t5 \/ M F2 H
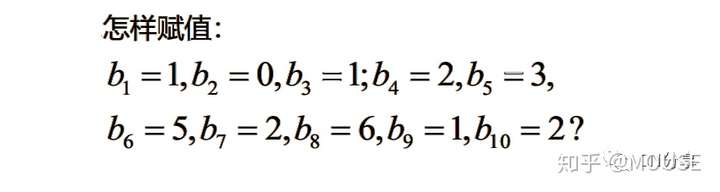 L( o7 C* J* ~" _$ J, S& E9 D
L( o7 C* J* ~" _$ J, S& E9 D
code:
sets:!集合段;ss/1..10/:b;endsetsdata:! 数据段;b=1 0 1 2 3 5 2 6 1 2;enddata
. ]5 p3 }2 L; @/ n 9 n# U% ~) X: P; y& O
9 n# U% ~) X: P; y& O
code:
sets:!集合段;a/1..100/:x;b/1..200/:y;Endsets!目标与约束段;@for(b(j):@gin(y(j)));@for(a(i):@bin(x(i));+ r0 b$ Q2 F0 e4 @; ^
派生集合派生集合就是派生出来的集合,看几个例子就懂了。
+ {( U6 v% T: @( d
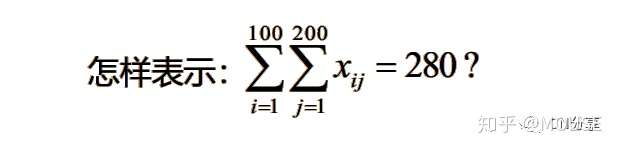 5 y/ n, j) n, g" r. F$ K0 K, H% A
5 y/ n, j) n, g" r. F$ K0 K, H% A
code:
sets:a/1..100/:;b/1..200/:;C(a,b):x;!派生集合;Endsets!目标与约束段;@sum(c(i,j):x(i,j))=280;
, m) R* s; I& \$ Q& W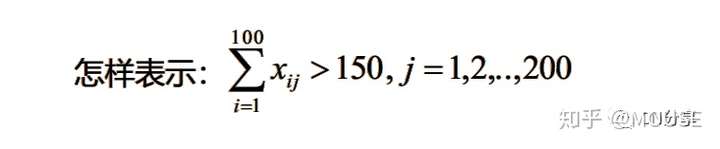
6 _% u! g: e3 ] W8 V! acode:
sets:a/1..100/:;b/1..200/:;C(a,b):x;Endsets!目标与约束段;@for(b(j):@sum(a(i):x(i,j))>150.001);!集合元素的循环函数;1 s7 n+ B1 U* f2 w9 P
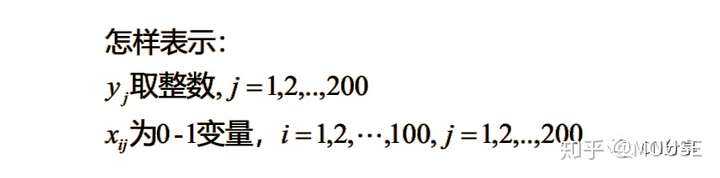
2 o3 O$ o' ?3 Ucode:
sets:a/1..100/:;b/1..200/:y;C(a,b):x;Endsets!目标与约束段;@for(b(j):@gin(y(j)));@for(c(i,j):@bin(x(i,j));
9 p# H- z [5 f逻辑运算符与过滤条件这个前面提到过,再罗列一次:5 E$ P% `4 h3 U. h9 [7 K6 V# ^) b
LINGO逻辑运算符有9种:9 b7 l- y' {5 g
#AND#(与),#OR#(或),#NOT#(非):
6 T5 d& C/ P! [* F) Z( `' }0 h1 P#EQ#(等于),#NE#(不等于),
) h) z1 f7 h1 k* }#GT#(大于),#GE#(大于等于),
9 j, T& ?' X+ Z, f* q; c#LT#(小于),#LE#(小于等于)2 G( f7 `$ B9 P
看下面一个例子:$ E! K' r% m9 p+ H. ~# p
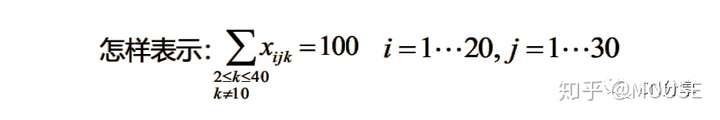
3 i# C ~# n% y; Acode:
sets:a/1..20/:;b/1..30/:;C/1..40/:;d(a,b,c):x;Endsets!目标与约束段;@for(a(i):@for(b(j):@sum(c(i,j,k)|k#gt#1#and#k#ne#10:x(i,j,k))=100));!过滤条件;
% p, \& S+ l( P$ e4 l: A如果我们表示一个分段函数时,就可以是if函数
@IF(logical_condition, true_result, false_result)- [( ~ z% }/ U) T7 {3 D6 S9 @* c! T
当逻辑表达式logical_condition的结果为真时,返回true_result,否则返回false_result。

. V) M# n& T4 R+ e6 j! kcode:
f=@IF(X#LE#500,4*X,@IF(X#LE#1000,500+3*X,1500+2*X));
' `' B3 B3 a- l* I掌握上述方法,可以解决掉大部分规划问题,如果还想进一步了解,可以去查阅相关书籍。
实际应用线性规划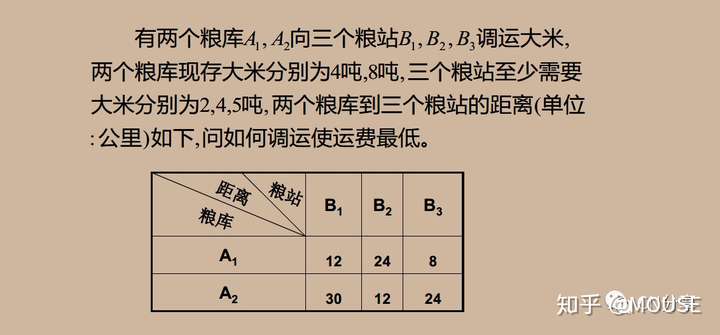 ; G7 p' }$ c2 ^5 B4 b4 I
; G7 p' }$ c2 ^5 B4 b4 I
原运输问题变量更换为:
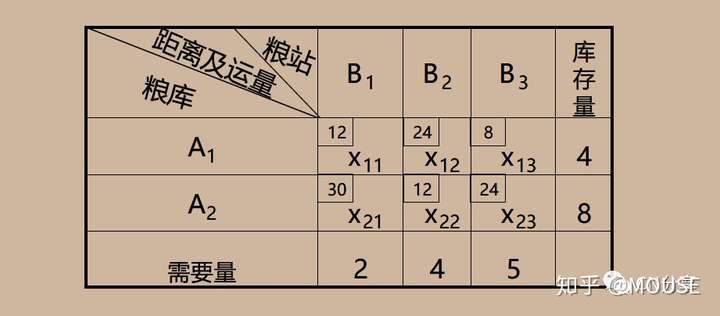
0 Y8 N4 g/ ]/ N! I$ j4 h3 @建立模型为:
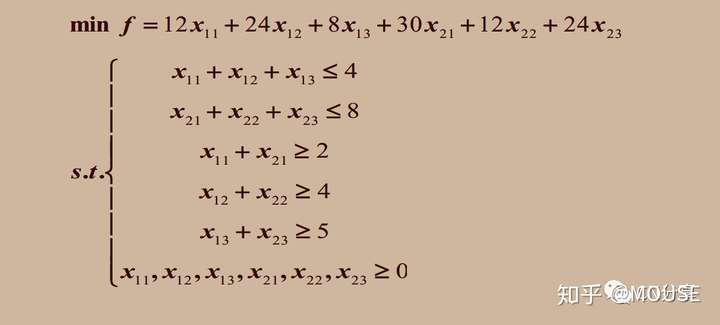 ( X. b D3 D" |5 |
( X. b D3 D" |5 |
模型进一步转化为:
 ) _/ t/ @% \# R* h$ H$ \
) _/ t/ @% \# R* h$ H$ \
程序编写:
MODEL:TITLE 调运大米的运输问题程序3;!定义集合段;SETS IANGKU/1..2/:A;!定义粮库的集合;LIANGZHAN/1..3/:B;!定义粮站的集合;YULIANG(LIANGKU,LIANGZHAN):X,C;!定义运量和距离;ENDSETSDATA:!粮库到粮站的距离;C=12 24 830 12 24;!粮库的限量;A=4 8 ;!粮站的限量;B=2 4 5;ENDDATAMIN=@SUM(YULIANG:C*X);!粮库上限的约束;@FOR(LIANGKU(I):@SUM(LIANGZHAN(J):X(I,J))<A(I));!粮站下限的约束;@FOR(LIANGZHAN(J):@SUM(LIANGKU(I):X(I,J))>B(J));END
IANGKU/1..2/:A;!定义粮库的集合;LIANGZHAN/1..3/:B;!定义粮站的集合;YULIANG(LIANGKU,LIANGZHAN):X,C;!定义运量和距离;ENDSETSDATA:!粮库到粮站的距离;C=12 24 830 12 24;!粮库的限量;A=4 8 ;!粮站的限量;B=2 4 5;ENDDATAMIN=@SUM(YULIANG:C*X);!粮库上限的约束;@FOR(LIANGKU(I):@SUM(LIANGZHAN(J):X(I,J))<A(I));!粮站下限的约束;@FOR(LIANGZHAN(J):@SUM(LIANGKU(I):X(I,J))>B(J));END
6 M2 C$ o' X4 b I运行程序即可得到结果。
非线性规划CUMCM2004C请你参考下面给出的数据(或自己收集资料)建立饮酒后血液中酒精含量的数学模型,并讨论以下问题:
- 对大李碰到的情况做出解释;
- 。。。5 \6 Z+ Q( o* \, O3 M
参考数据
- 。。。
- 体重约70kg的某人在短时间内喝下2瓶啤酒后,隔一定时间测量他的血液中酒精含量(毫克/百毫升),得到数据如下:1 X& m# N/ C/ i8 M6 X# a
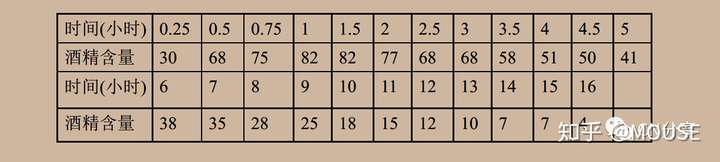 2 H- W# G$ W6 Z- D
2 H- W# G$ W6 Z- D
分析:把人体内酒精的吸收,代谢,排除过程分成两个“室”,胃是第一个室,血液为第二室,酒精先进入胃,然后被吸收进入血液,由循环到达体液内,再通过代谢,分解及排泄,出汗,呼气等方式排除。; Y. C6 @" [) ]- d) [2 `
假设胃里的酒精被吸收进入血液的速度与胃中的酒量x(t)成正比,比例常数为k1,血液中的酒被排除的速度与血液的酒量y(t)成正比,比例系数为k2,G0为短时间内喝入胃的酒精总量,则可以建立微分方程:
9 w; ]. w* F4 T/ j; f/ R
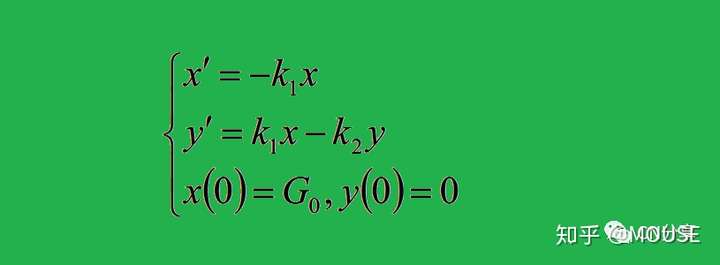
求解得:8 X) A6 c% c1 A% o0 h
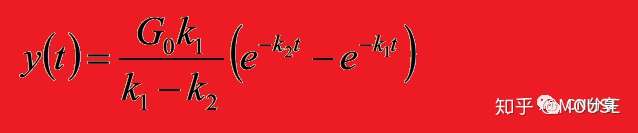
变换为:
; v# z' h" G: V4 S) \
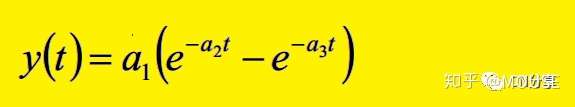
0 ?, F8 ]3 V- Y/ ~) y$ M l, p因而问题就可以转化为:
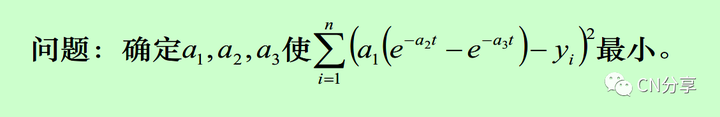
( o- f" u. s: h编写程序:
MODEL:SETS:BAC/R1..R23/:T,Y;ENDSETSDATA:T=0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 1415 16;Y=30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 77 4;ENDDATAMIN=@SUM(BAC A1*(@EXP(-A2*T)-@EXP(-A3*T))-Y)^2);END$ ^4 m) r0 G6 y c5 O/ F9 `
A1*(@EXP(-A2*T)-@EXP(-A3*T))-Y)^2);END$ ^4 m) r0 G6 y c5 O/ F9 `
运行程序,即可获得结果。
整数规划:对上次最后一个题目,用Lingo进行求解。5 N0 |+ G+ g! {& o) o3 v
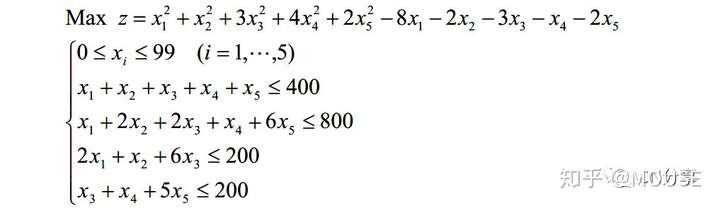
编写程序:
model:sets:row/1..4/:b;col/1..5/:c1,c2,x;link(row,col):a;endsetsdata:c1=1,1,3,4,2;c2=-8,-2,-3,-1,-2;a=1 1 1 1 11 2 2 1 62 1 6 0 00 0 1 1 5;b=400,800,200,200;enddatamax=@sum(col:c1*x^2+c2*x);@for(row(i):@sum(col(j):a(i,j)*x(j))<b(i));@for(col:@gin(x));@for(col:@bnd(0,x,99));end
2 r) W- Y, P- h# ^% a运行即可求出结果,还是满精确的。
9 w/ r" F, o+ U, U
0 {6 k7 d+ M4 x3 Z) ^
| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) |
Powered by Discuz! X2.5 |



 : Z* J0 d. X! L1 T# Y
: Z* J0 d. X! L1 T# Y
 运算符
运算符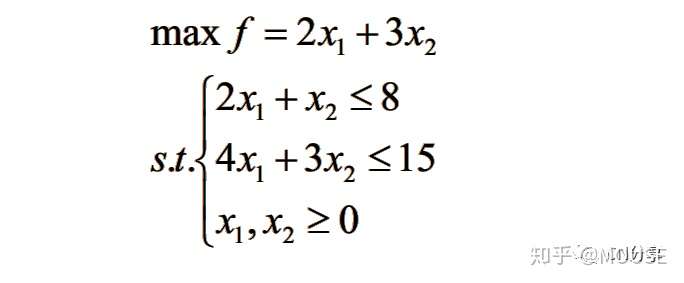

 1 \, C( }& |( K6 N5 D/ ^& t% t, D5 U
1 \, C( }& |( K6 N5 D/ ^& t% t, D5 U ) p. a9 L, ~( n( t! f
) p. a9 L, ~( n( t! f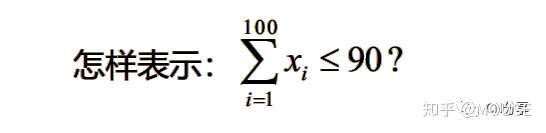
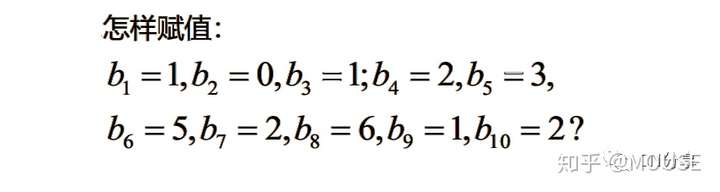 L( o7 C* J* ~" _$ J, S& E9 D
L( o7 C* J* ~" _$ J, S& E9 D 9 n# U% ~) X: P; y& O
9 n# U% ~) X: P; y& O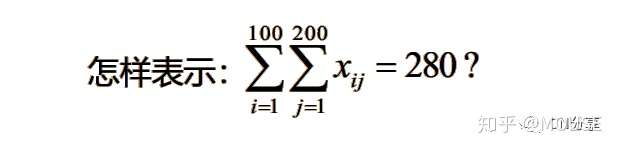 5 y/ n, j) n, g" r. F$ K0 K, H% A
5 y/ n, j) n, g" r. F$ K0 K, H% A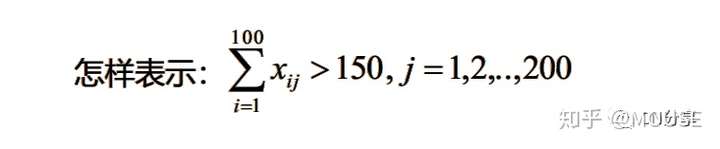
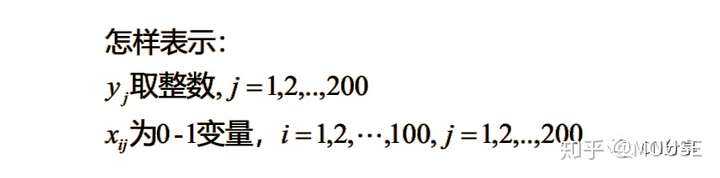
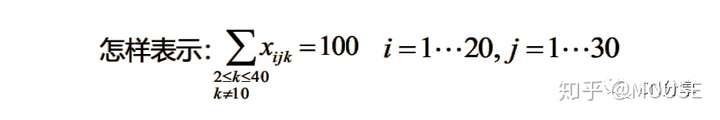

 ; G7 p' }$ c2 ^5 B4 b4 I
; G7 p' }$ c2 ^5 B4 b4 I
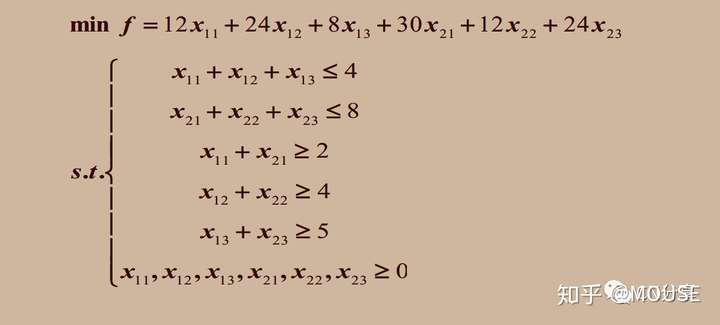 ( X. b D3 D" |5 |
( X. b D3 D" |5 | ) _/ t/ @% \# R* h$ H$ \
) _/ t/ @% \# R* h$ H$ \ IANGKU/1..2/:A;!定义粮库的集合;LIANGZHAN/1..3/:B;!定义粮站的集合;YULIANG(LIANGKU,LIANGZHAN):X,C;!定义运量和距离;ENDSETSDATA:!粮库到粮站的距离;C=12 24 830 12 24;!粮库的限量;A=4 8 ;!粮站的限量;B=2 4 5;ENDDATAMIN=@SUM(YULIANG:C*X);!粮库上限的约束;@FOR(LIANGKU(I):@SUM(LIANGZHAN(J):X(I,J))<A(I));!粮站下限的约束;@FOR(LIANGZHAN(J):@SUM(LIANGKU(I):X(I,J))>B(J));END
IANGKU/1..2/:A;!定义粮库的集合;LIANGZHAN/1..3/:B;!定义粮站的集合;YULIANG(LIANGKU,LIANGZHAN):X,C;!定义运量和距离;ENDSETSDATA:!粮库到粮站的距离;C=12 24 830 12 24;!粮库的限量;A=4 8 ;!粮站的限量;B=2 4 5;ENDDATAMIN=@SUM(YULIANG:C*X);!粮库上限的约束;@FOR(LIANGKU(I):@SUM(LIANGZHAN(J):X(I,J))<A(I));!粮站下限的约束;@FOR(LIANGZHAN(J):@SUM(LIANGKU(I):X(I,J))>B(J));END 2 H- W# G$ W6 Z- D
2 H- W# G$ W6 Z- D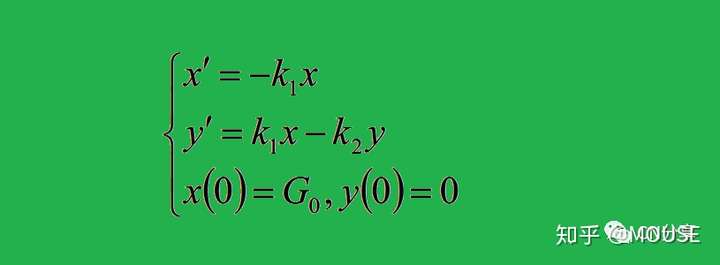
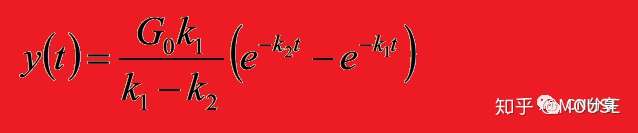
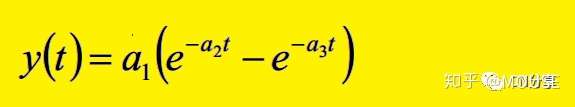
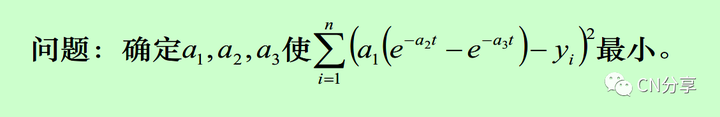
 A1*(@EXP(-A2*T)-@EXP(-A3*T))-Y)^2);END$ ^4 m) r0 G6 y c5 O/ F9 `
A1*(@EXP(-A2*T)-@EXP(-A3*T))-Y)^2);END$ ^4 m) r0 G6 y c5 O/ F9 `