数学建模社区-数学中国

标题: 哪些控制类的算法惊艳了你？ [打印本页]
作者: 杨利霞    时间: 2020-6-8 15:18
标题: 哪些控制类的算法惊艳了你？
哪些控制类的算法惊艳了你？

作者：运筹OR帷幄
链接：https://www.zhihu.com/question/26944678/answer/1155702519
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

深度强化学习(DRL）的一炮走红，让人们一谈起强化学习首先想到的往往是DRL，而强化学习最早的起源来自 optimal control theory 。LQR和iLQR 作为最优控制/基于模型的强化学习算法，在环境动态系统已知的情况下能更加高效的利用样本，并在化工生产过程，无人驾驶，机械臂控制等实际应用场景取得了很好的效果。

回答提纲：
背景强化学习（RL）本质上是一种控制算法。大多语境下RL都是指无模型的RL算法，而依赖于模型的控制方法LQR、MPC等被归为有模型的RL，他们的假设是环境的动态特性已知。基于模型的RL往往被认为有更高的样本利用效率。我们将介绍常见的最优控制/轨迹优化算法LQR(线性二次型调节器)及其非线性版本iLQR(迭代LQR)算法。有意思的是，LQR问题在离散时间情况下其实是通过动态规划来解的。本文的算法介绍包含三部分内容 i）LQR ii）iLQR iii）iLQR的改进
任务定义解决方案LQR注意，其中C矩阵是根据实际控制需求人为设定的，F是已知的。
明确一下，我们的目标，找到使得（3）最小的轨迹。由于环境和cost是已知的，我们不需要进行无模型RL中的探索环节，通过规划（planning）即可得到最优策略和动作。解决LQR问题的方法即是借鉴动态规划算法，求解思路如下：
1）看最后一步，得到子问题。
2）求子问题最优解。
3）根据状态转移(模型)，得到包含已求解过的子问题的新子问题
4）跳转到2），直到递推到第一步结束。
LQR算法流程如下：
iLQR这里iLQR中的“迭代”不是动态规划中的迭代，倒是和牛顿法里面的迭代过程非常相似，我们知道梯度下降是利用泰勒展开的一阶项去近似原函数迭代求下一个值，而牛顿迭代是利用二阶项去近似原函数，模型更准确，收敛更快。和iLQR有什么关系呢？先来看一下如何应对非线性。它将非线性的环境和cost函数，通过泰勒展开局部线性化，之后通过LQR的barkward过程解出线性化环境、cost下的“最优解”。但是，这得到的“最优解”并不是我们想要的最优轨迹，因为类似于牛顿迭代，LQR backward整个过程的等同于求导，只是对此时x0处展开的函数求极值（红色下划线部分），而该部分与和原函数是有误差的，得到的新坐标x也与只能通过一步步迭代逼近最优解。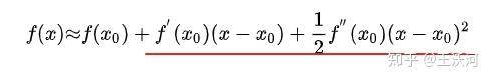
二阶泰勒展开忽略高阶项
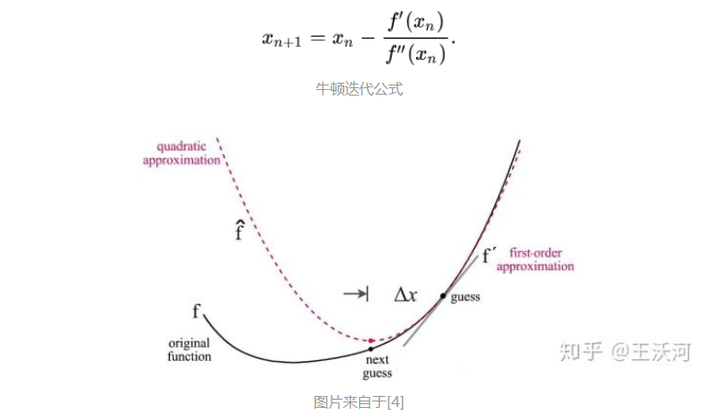图片来自于[4]
准确而言，iLQR是微分动态规划（DDP）的变种，iLQR对应于高斯-牛顿法，而DDP对应于（全）牛顿法。之后会进行辨析。
iLQR算法可以分为线性化，LQR backward和forward三部分。
在iLQR中环境动态展开成一阶，cost展开成二阶。而微分动态规划（DDP）则是将环境动态也展开成二阶。前者会使得计算简单，但是丧失了二阶收敛性。后面iLQR的改进版本[1]里面会提到改进版本。
论文[1]中是采用另外一种方式，直接线性化Q函数，对其进行二阶泰勒展开，得出来的结果与上面是相同的。（15）看起来有点陌生，其实是泰勒展开时f(new guess)-f(old guess)，即移项后的结果。
要注意，forward的时候要和真实的非线性系统进行交互，得到真实轨迹，而不是与线性化模型交互。
算法流程如下：
iLQR的改进文献[1]对以上iLQR算法作出几点改进，伯克利的Guided Policy Search[2]中也采用该方法来作为强化学习的引导策略。
（1）引入模型预测控制的思想
模型预测控制（MPC, Model predicitve control）是一种常用的控制算法，根据对环境建立的预测模型，可以进行在线轨迹优化，过去被使用在动态响应比较慢和平稳的化工过程控制当中，近些年在机器人控制中也成为了主流。MPC有如下几个特点：
1）预测模型
有对环境的建模，模型可以是任何形式，包括非参数模型以及参数模型（如CARIMA模型、神经网络、传递函数等）。由于下面第2)点的存在，预测模型可以不用十分精确。
2）滚动优化
MPC是在滚动时域（receding horizon）内进行轨迹优化，它的优化目标是当前区域内的，和全局优化目标不一样。MPC同样也不是像LQR一样离线进行的，而是在线地沿时间轴反复进行——滚动优化，也是和传统最优控制根本区别。
3）反馈校正
MPC一步优化完成以后，得到未来时域内的最优动作序列，但是一般只实施第一步动作，而非全部，然后重新收集反馈信息。这样可以防止模型失配或者环境干扰引起控制性能下降，提高其鲁棒性。
在这篇文献中，作者就是将MPC这三个机制，引入到了DDP/iLQR中。首先是预测模型，不同于之前iLQR里面的非线性动态是实际环境，在这里，用于iLQR计算的非线性动态只是真实环境的一个模型。其次，滚动优化，这里不再是一次性的算出整条最优控制轨迹，而是只用iLQR算出一段时间之内的轨迹，每次仅仅在真实环境中实施第一步。并且，每一步都收集新的反馈，用于下一步的重新规划。
值得一提的是，我们回到之前说的DDP和iLQR主要的区别就在于前者用了环境动态的二阶导，而后者没有。这使得iLQR虽然计算加快了，但是失去了二阶收敛性。但是在模型预测控制（MPC）的场景下，由于是滚动优化，滚动时域上的收敛性从来没有真正的被满足过，所以改进后的iLQR为了速度提升牺牲一定的收敛性完全没问题。
（2）改进regularization term
（3）改进line search

代码及实现https://github.com/navigator8972/pylqr
neka-nat/ilqr-gym
https://www.mathworks.com/matlabcentral/fileexchange/52069-ilqg-ddp-trajectory-optimization

参考文献
说明：
本文的推导过程主要来自于伯克利CS285课程[3]和[4]
[1] Tassa Y, Erez T, Todorov E. Synthesis and stabilization of complex behaviors through online trajectory optimization[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2012: 4906-4913.
[2] Levine S, Koltun V. Guided policy search[C]//International Conference on Machine Learning. 2013: 1-9.
[3] Course: CS285 | EECS at UC Berkeley
[4]https://medium.com/@jonathan_hui/rl-lqr-ilqr-linear-quadratic-regulator-a5de5104c750








欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) Powered by Discuz! X2.5