 : a. y$ l2 t( J+ U$ [1 v8 }' F% y
: a. y$ l2 t( J+ U$ [1 v8 }' F% y 9 s! @% Y; n* m: ~
9 s! @% Y; n* m: ~
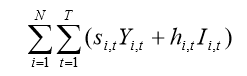 ( 1 )
( 1 )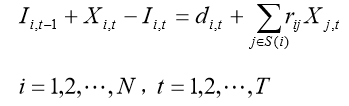 ( 2 ) 1 e Z' U* c" ? U4 X& `
( 2 ) 1 e Z' U* c" ? U4 X& `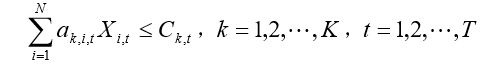 ( 3 )
( 3 )  ; g9 a" h( t* v6 j. I
; g9 a" h( t* v6 j. I

 emand,X,Y,Inv;
emand,X,Y,Inv;  BIN(Y));
BIN(Y)); 
| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) | Powered by Discuz! X2.5 |