数学建模社区-数学中国
标题: 【R语言】回归分析案例:北京市商品房价格影响因素分析 [打印本页]
作者: 1047521767 时间: 2021-10-27 14:50
标题: 【R语言】回归分析案例:北京市商品房价格影响因素分析
【R语言】回归分析案例:北京市商品房价格影响因素分析4 H. [4 d7 ^) K& P1 C4 M8 y! g; B4 |& `
这一案例是王汉生老师《应用商务统计分析》方差分析章节的案例,主要对离散型变量进行了处理。
9 R( v4 z2 k" s这里将连续型变量也加进来,进行协方差分析,建立完整的模型。
首先对房价进行对数变换,解决异方差问题:

3 Q$ v$ l$ Z9 [% {7 r' E% `7 P行描述性统计分析,各连续型变量之间的相关关系如下:9 `) p' x& v5 f! z; m
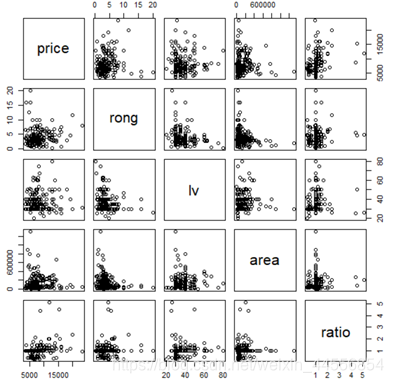
$ o+ _2 l" k; X名义变量的EDA一般做箱型图。
模型按照全模型-变量处理(分箱等)-变量选择-回归诊断等步骤建立。
9 ^! d. @& }. S* w
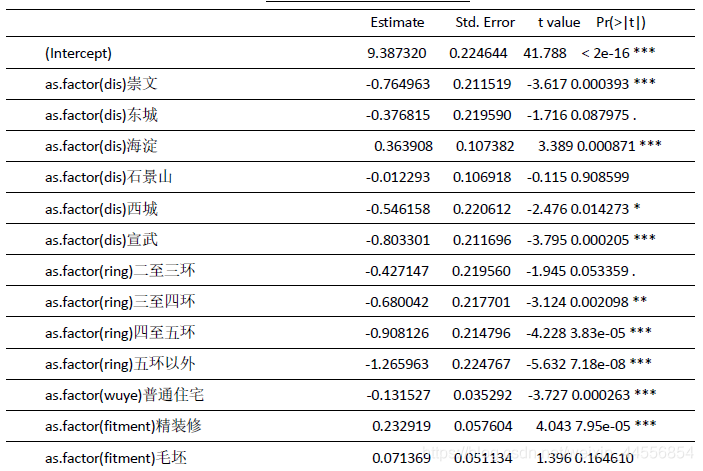 6 Z1 T9 L. i5 O4 A& \8 `3 }
6 Z1 T9 L. i5 O4 A& \8 `3 }
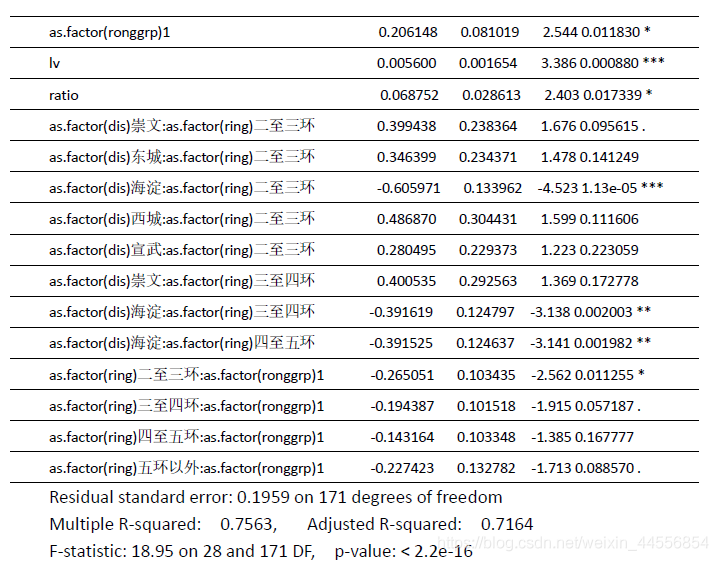 6 C( h% v- T9 X4 P( ~* L' D
6 C( h% v- T9 X4 P( ~* L' D
最终模型残差图:
1 j" h/ {( W. q( a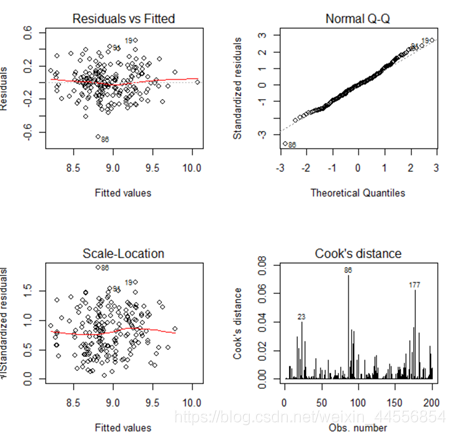
. c$ F T: d/ J$ L通过模型分析结果可知,影响北京市商品房平均销售价格的主要因素有:! b' b6 q* d8 i8 d# ?1 B% a( \
属性变量:所在辖区、所在环线、物业类别、装修状况、容积率大小(新引入);连续变量:绿化率、停车位住户比2 D6 e) C; v' U# ^$ e
属性变量的具体影响在此处分析略去。5 H9 M& a4 a. Q o
连续型变量的影响主要为:
8 N3 j' N r6 ^0 S6 A* N" S 绿化率:绿化率的影响十分显著,由系数估计值为正,说明对房价有正向影响,绿化率越高的楼盘房价越高;
# b) ?) m6 P, C3 T0 Q5 {/ l& \ 停车位住户比:有较显著的影响,停车位住户比越高,价格越高;; G* Q8 }) O% U& p: K" S- c7 k
同时,原本为连续型变量的容积率经过离散化变为属性变量后:
% B9 k7 V R0 k) R8 B+ U 容积率大小:容积率分组有较显著的影响,高容积率的小区商品房价格更贵;
7 _$ O' N0 [" I& g7 i# X 容积率与环线之间存在着交互效应。+ B; R$ V0 [' t0 e6 q
rm(list=ls()) #清空当前工作空间
4 c$ J- p' Z0 a _* J* psetwd("D:/回归分析")
+ I/ x3 w) c a! ~" |+ D( {: x3 ~. Ia=read.csv("real.csv",header=T) #读入csv格式的数据,赋值为a
6 g2 g8 d. A0 UView(a)5 o. C" Q: } g
attach(a)4 c8 t6 J' p C7 c+ ~9 A7 ?
names(a)
; o1 O5 E8 q% Q5 S$ l; u$ _( G3 m! C9 a2 u
8 o+ w5 {+ c) ^2 E, W
##描述性统计
0 z' J; O+ i7 R4 e' {6 ~5 ?7 s2 b* g" p) s# V& l
5 c8 A9 k; p% s9 }0 w#未做处理的响应变量分布情况+ t+ T' q/ @$ V# {9 g
par(mfrow=c(1,1))( P' r) s9 A2 x$ S- l
hist(price)
. x, ~1 m' ?/ i3 }- V) {9 ?3 |summary(price) #查看响应变量的描述统计量% [4 }2 D4 s# q* K
#连续型变量描述性统计
# v0 B. R8 m3 q' N% X. r3 \$ X! _windows()
. }- |5 C8 |! n3 J, qpairs(a[,c(6:10)]) #所有连续型变量间的散点图
% W5 X4 J! F* Lpar(mfrow=c(2,2)) . i1 ?( f/ ~! B7 u W7 c9 r
plot(rong,price) #每个连续型因变量与响应变量间的散点图) K" i* @( y+ }1 j: [; X K
plot(lv,price)% @/ W) S# \2 }5 E
plot(area,price)
+ n7 P3 ~4 N7 L0 E* W2 H$ Lplot(ratio,price)6 B* o) v' f; w# ~6 \& `
summary(a[,c(6:10)]) #查看连续型变量的描述统计量
2 N# Y6 O6 [# ]9 D( vcor(a[,c(6:10)]) #查看连续型变量的相关系数
$ r, \) @; ]% m! t* u) R#属性变量描述性统计
" G9 P2 a% l3 U. [. h: @: r+ Jwindows()* X; w. t+ _! R/ [' A N: U
par(mfrow=c(2,3))
( h& k: y3 V( E0 R7 bboxplot(price~dis) #每个属性变量关于响应变量的箱型图
" Z: L# v8 P! G* Bboxplot(price~wuye) + @- u( X5 Y# u% k. D/ _1 c2 V
boxplot(price~fitment)
4 [. c7 E6 D/ c; ]! {1 `4 a5 Dboxplot(price~ring) , n7 x, @# G) y
boxplot(price~contype) l* Z# z" N% y+ d) ^ q
+ K8 |$ ^0 v5 K( O7 c# G) I8 u
# n. \; `. t( n: F N4 @: ~
% l0 C' p3 O% S/ J/ l M% W
. c+ \2 \1 P4 N##模型建立, `* b1 i0 @, |1 `
0 y* I- B. F0 @% d
/ a6 X) z! `( ~: Q6 U+ }8 A#在方差分析模型基础上加入连续型变量! u6 c+ J4 _* j5 c
lm1=lm(price~as.factor(dis)*as.factor(ring)+as.factor(wuye)+as.factor(fitment)+as.factor(contype)+rong+lv+area+ratio)9 c3 d& m2 S6 }+ t; }) A2 t
anova(lm1) #方差分析8 H o/ L) o. F" {" A, k- r
summary(lm1) #模型参数估计等详细结果
: w0 `' x% T7 |- \: Ywindows()3 g& X5 l/ }2 P" W& G+ _: g
par(mfrow=c(2,2))
/ a4 ~9 x/ K! ^plot(lm1,which=c(1:4)) #回归诊断做残差图; V$ ~5 ]2 y' Z. e5 V( W0 I
; E7 n( |. G/ w
) c" J' K: T9 q% c
5 q1 n1 a& M/ \" b J, M! c3 Q( V4 F$ ~2 F' ^
##变量处理* X, J9 E. A. Q$ j" ~; j1 g, `( e
7 _" j! ^+ h7 a
* F. u7 Q& Q9 J& X$ \$ T, y" D( d###对不显著的变量采用分组的方式希望能达到显著的效果
6 m! z! a, f& A Z5 r% ^( s" E##对容积率的处理 H3 Q% |* L U0 x$ h
windows()* g# s1 k5 _# B# q
n = 48 I" b# o3 O9 l
boxplot(price~ceiling(rong/n)) #容积率多分组下的箱型图 ) b6 u7 W2 o4 o& f1 M& p
table(ceiling(rong/n)) #容积率各分组下的样本数# a: R1 z. T! j$ y. k; Z4 g
ronggrp=1*(rong>n) #进行二分类3 W2 f( i6 C' t
#ronggrp=ceiling(rong/n)
7 b* y2 R" S \) Q% gtable(ceiling(ronggrp)) #容积率二分类下的样本数+ f# _7 [( _# t: e& x
windows()+ z' G7 ?5 _7 V: y1 P/ f5 h* V# U
boxplot(price~ceiling(ronggrp)) #容积率二分类下的房价箱型图- H( w7 a! y* g0 B" ^
windows(): U$ I- \. r4 s% Z
par(mfrow=c(1,2))
- \% \/ O; m; L" Cboxplot(rong~ring) #容积率与环线箱型图3 M3 T: o1 Z: q/ d
boxplot(price~ring) #房价与环线箱型图 b& N! P4 P X4 W h j
#加入容积率分组和容积率分组*所在环线交互因子的模型
2 q9 V; b3 j; f: l; elm2=lm(price~as.factor(dis)*as.factor(ring)+as.factor(wuye)+as.factor(fitment)+as.factor(contype)+as.factor(ring)*as.factor(ronggrp)+lv+area+ratio)
; \: }' S% R+ ~+ r0 Z6 panova(lm2) #方差分析
- g% I# l8 V0 F6 `- fsummary(lm2) #模型参数估计等详细结果7 n- A: w" c3 e: ]
windows()' r" u# ~8 U8 C: u- P; E3 \8 M
par(mfrow=c(2,2))
8 f* ]- @7 R8 K+ Jplot(lm1,which=c(1:4)) #回归诊断
2 l$ A9 B4 T# Y" [4 J5 D
! E3 D& r" Q, A- n
: y6 h( c6 {4 H9 c; g##对小区面积的处理$ p% K H( t" |& \9 h
summary(area)
8 A6 L: v$ L: F; X" F( ~; G) gplot(area,price)
' w3 q1 c4 Q; [3 {' s5 i0 ~! nwindows()
: g. g1 W, @$ S u+ Qn = 150000
/ W$ N) A L9 B m! Q1 J5 Z. gboxplot(price~ceiling(area/n))
6 E) O$ T3 Z6 d( G" r& v. K( itable(ceiling(area/n)) . h/ \1 E5 k! d2 y: ]+ ~: O, ^, R
areagrp=1*(area>n)5 X' Y7 F0 Y% d
table(ceiling(areagrp)); D# M6 u: Z0 v' F J2 t; u: u( V0 G
boxplot(price~ceiling(areagrp))2 Z5 W$ L* v9 k9 [' ?5 z5 i
#加入小区面积分组的模型
( w6 Z' F4 H2 T( Y- J6 slm3=lm(price~as.factor(dis)*as.factor(ring)+as.factor(wuye)+as.factor(fitment)+as.factor(contype)+as.factor(ring)*as.factor(ronggrp)+lv+as.factor(areagrp)+ratio)
5 Y4 X% i6 Q$ k$ J5 r: uanova(lm3) #方差分析5 Z1 Z; K' Z& o m' d+ d5 m
summary(lm3) #模型参数估计等详细结果4 D! ?8 O: g: X+ T% x3 q# N, r8 J
windows()
+ y$ |& C" k# c& s6 Mpar(mfrow=c(2,2))
7 I! E4 m% j: y }plot(lm3,which=c(1:4)) #回归诊断
3 d, t: _) ~* ^, j$ Z
( B* R! e7 b3 U& |
* \$ t& q4 B5 Y0 g0 ?' a##变量选择
( x; x+ o7 ]3 D; C" v
7 Y# B7 p9 W9 O/ ?
% P9 i; Q* Z2 _& ?$ q: x! P. ]##AIC准则下的变量选择
/ m9 T7 I( v' hlm4.aic=step(lm3,trace=F) #根据AIC准则选出最优模型,并赋值给lm.aic
1 x" f/ y3 e. ?. I( Rsummary(lm4.aic) #给出模型lm.aic中系数估计值、P值等细节
# X( R# O) @) R1 y##BIC准则下的变量选择
. w% w, t/ |: }9 P7 w6 [lm5.bic=step(lm3,k=log(length(a[,1])),trace=F) #根据BIC准则选出最优模型,并赋值给lm.bic
6 l+ _1 I8 n1 U0 Ysummary(lm5.bic) #给出模型lm.bic中系数估计值、P值等细节
7 l2 L. D! O3 Z
$ ~4 K, C/ @! q3 M6 |% f' L
6 q/ v- W3 x: Y#选用AIC准则下的模型进行回归诊断
. U+ @% f8 {2 w1 f. L: a8 qwindows()& }# ^6 w0 o( F) L
par(mfrow=c(2,2))" o( M6 l6 ?) K, K7 {/ a, `# Z6 M
plot(lm4.aic,which=c(1:4)) ( U1 x6 x1 v0 y1 w, B; y0 Z
6 a8 d! l# i- H) q- ]
, i" @7 J% V1 U! ?3 s
% J7 s- F* L4 `8 G( t$ J$ X- C4 |% T, @: v2 S8 k9 F& i
##数据变换
5 N% A9 @% H% a I
0 l- U& G) H$ n* p5 @
+ ?+ m/ ^* w# u% s#box-cox变换
, D/ j3 M! G( O; R8 S3 @library(MASS)
" _$ M8 d; K$ R5 B- pb=boxcox(price~as.factor(dis)*as.factor(ring)+as.factor(wuye)+as.factor(fitment)+as.factor(ring)*as.factor(ronggrp)+lv+ratio, data=a,lambda=seq(-3, 3, by=0.1))6 b" ?, W" G7 f3 O
I=which(b$y==max(b$y)) #定位似然函数最大的位置
5 D0 e( l& S3 X [. H1 S* `9 s+ f" Olambda = b$x[I] #精确的λ值" x8 b$ [. E$ L' a% ~' j
#λ接近于0,为模型简洁性,可以直接进行对数变换
& [, @. v: d/ A2 i* W: ?logprice <- log(price)' Q* x7 Y* L& M! a
hist(logprice)
# A0 L3 a" Q) X
0 f; y. i. d4 F6 G/ K& o6 o9 ~. ^/ Z( J- v3 i& l" N# ~
##最终模型与诊断
2 u8 V( ]/ e1 x7 k
4 {+ z3 i) P- C# ?7 }/ w" t& r" p
lm6=lm(logprice ~as.factor(dis)*as.factor(ring)+as.factor(wuye)+as.factor(fitment)+as.factor(ring)*as.factor(ronggrp)+lv+ratio)
) o- V* U8 j2 s/ _' D( y1 o" E7 Pwindows()- G( L6 p* J/ q8 |2 H
par(mfrow=c(2,2))
- z/ Q5 X j Lplot(lm6,which=c(1:4))
, A5 h$ `* S, G0 C! n" b$ Qanova(lm6)
& D7 d8 W4 R; Q5 y2 osummary(lm6)6 _7 e5 O; C* e+ R5 p1 R
6 w. }2 ~* ]) A# @0 l
2 g0 ^4 l$ c4 A6 r请关注数学中国网微博和数学中国公众号,联系QQ 3243710560" a7 A9 M0 N3 R+ h
. _9 k1 U7 e) T2 h- S
- q! b( u# a3 G6 @& \) Q
3 f, I3 G2 ^ l4 o
: i: {" ^* c4 z
作者: fgfroom214 时间: 2021-10-27 16:32
一定会认真的看看,发现这是R的,有python的分析没有
$ S7 \5 O6 p, ?; v# l
0 c1 ]7 ?% h! _" N% x! ?) `
作者: sjlxdn 时间: 2021-10-27 19:55
111111111111111( a; j+ @- j2 O
作者: fgfroom214 时间: 2021-10-27 23:18
太好了,又认真的看了一次,发现自已差太多了7 t) V! O9 e; z+ X
. p) [' R c0 g0 n
作者: 1047521767 时间: 2021-10-28 11:01
fgfroom214 发表于 2021-10-27 23:18  ; Y2 u& C) d5 C' }3 ~* v. Q- F: _/ Q+ W
; Y2 u& C) d5 C' }3 ~* v. Q- F: _/ Q+ W
太好了,又认真的看了一次,发现自已差太多了
1 A, e. N; B7 H我每天会发一些好资源的
# ^' _' U" o' ?4 U& M1 R
作者: 1047521767 时间: 2021-10-28 11:01
fgfroom214 发表于 2021-10-27 16:32 
; c$ l8 _( O0 y+ Y! T7 \, o6 _+ `一定会认真的看看,发现这是R的,有python的分析没有
有啊
1 y; h; n" Z' Z- t
| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) |
Powered by Discuz! X2.5 |
; Y2 u& C) d5 C' }3 ~* v. Q- F: _/ Q+ W


 6 Z1 T9 L. i5 O4 A& \8 `3 }
6 Z1 T9 L. i5 O4 A& \8 `3 } 6 C( h% v- T9 X4 P( ~* L' D
6 C( h% v- T9 X4 P( ~* L' D