数学建模社区-数学中国
标题: 排序算法之冒泡排序 [打印本页]
作者: 1047521767 时间: 2021-10-29 20:30
标题: 排序算法之冒泡排序
排序算法之冒泡排序4 s( {5 L5 w2 N9 E
了解冒泡排序是什么！6 y( y1 R, M7 J+ ?! V4 y
知道冒泡排序的思路
8 ?+ G2 C* i5 ^知道实例代码并且练习
1 E! P' H$ X% \6 _5 N8 y8 y3 i有收获记得帮忙点个赞，有问题请指出。8 j9 C {4 h1 g9 r7 I
一、冒泡排序基本介绍
5 p4 U2 p: K" c4 \% m: x' @; ]- L1、冒泡排序（Bubble Sorting）的基本思想是：通过对待排序序列从前往后（从下标较小的元素开始）依次比较相邻元素的值，若发现逆序则交换，使值较大的元素逐渐从前往后移动，就像水底的气泡一样向上冒出。
4 g: H- [& G( j
- r m3 r1 \% h6 ~
) Y( a3 K* L5 Q0 V) h4 p2、冒泡排序的优化思路
4 p( \ \* H6 m7 t9 v! F- \因为排序的过程中，各个元素不断接近自己的位置，如果一趟比较下来没有进行交换，就说名顺序有序 ，因此要在排序过程中设置一个标志flag判断元素是否进行交换，从而减少不必要的比较。
: B- Q/ F4 E- y
* n x% {9 j% b2 G0 r7 W5 W& a7 N6 ]% {: N1 R4 n# r: J5 l, z
3、冒泡排序的图解思路
$ `" ?7 K! p( U9 L8 V4 X8 I! r9 h* g3 F( F1 v% p
^+ z: m; Y" h其实就是两个指针，移动来进行判断，然后如此循环进行比较 ，具体思路大致如下：. ~+ Y2 l* ^& a6 Q7 V2 H
6 o: b3 U& D, g" y
8 X' [2 M% b- e0 Z# ]
第一轮循环得到最大值
: ?! x9 K+ k) b, ]' L2 g0 |; w3 A第二轮循环得到第二大值! X( e& c$ G+ N0 o# j
第三轮循环得到第三大值
/ L- |- @9 y) A9 x$ f0 _$ O8 ~/ I# h5 e第四轮循环得到第四大值
; z o* y c! b# L总的要进行数组大小减1的词循环9 a0 f8 C% O7 c; m& \9 W# l
' b, Y$ M- g+ O. E
% v, h' V( f# j% {: U二、冒泡排序代码实现package cn.mldn;& A* z6 S- y$ S
, g$ Z: K* \. Y# M
; h( `5 Q. a1 L& u- c
import java.util.Arrays;4 ?+ ]! U. `7 j( V7 @7 O- E9 @9 b
& ?/ T% ?3 r- n. R
1 ^* t1 q# F0 X. F8 |$ V3 j
public class BubbleSort {& ?: J7 X: H3 a6 I2 E, X) u" L
public static void main(String[] args) {+ Y1 e9 t. L8 c: w
int[] arr = {3,9,-1,10,-2};
( [2 w7 T9 O5 D5 A5 Y //大致过程- M6 S( ?# b: @, q' Z9 o6 ?
//1、第一步就是第一轮排序得到最大值于最后
# a8 D( G3 |3 `& i" C4 f // for (int i = 0; i < arr.length - ; i++) {
6 Q7 Y0 [1 u( S# T // //如果前面的数比后面的数大，则交换
+ m; [# E" Q' U/ Z# S // if (arr > arr[i+1]) {
) {. ~- m% m7 Q // temp = arr;0 D+ e3 n; q# |
// arr = arr[i + 1];
h4 p6 `& Y( J. s0 j // arr[i + 1] = temp;4 A z$ F; w" C9 k% L5 X) \9 Q
// }- D5 K0 F6 v$ Z2 o/ N9 B
// }- B3 _/ v: b- v( z; g3 V
//2、第二糖就是把倒数第二大的排到倒数第二位
+ }+ Q0 o, [8 ?0 E2 |; |8 d. [ // for (int i = 0; i < arr.length - 1 - 1; i++) {4 K$ S! u" Q t5 v2 n; f+ j% j
// //如果前面的数比后面的数大，则交换
# Z" R0 _$ E: V // if (arr > arr[i+1]) {
3 U& L! {. X5 [ // temp = arr;
0 _# h, _$ y+ y/ H // arr = arr[i + 1];
% u+ n3 y9 X- }5 B // arr[i + 1] = temp;
$ n6 j, K% h' K0 C3 \% } // }" M& g. L* {4 _" t
// }2 l& I7 d" Q {; ]. o
//3、第三糖排序，以此内推& f4 N! [8 a2 ` J3 f) v
//for (int i = 0; i < arr.length - 1 - 1 - 1; i++) {9 E7 w7 z2 l9 H1 E2 J
// //如果前面的数比后面的数大，则交换5 Q! c" C9 c0 [- M) ~* e( Q0 [ }
// if (arr > arr[i+1]) {
3 @ o+ P6 N( S+ I // temp = arr;4 C: |3 c E, G$ R! J% y) Z
// arr = arr[i + 1];9 a! }/ d, T d
// arr[i + 1] = temp;
/ c1 n: d, E$ `3 R // }
% V8 c1 U- q+ ^% T // }+ ~2 ^/ J# D% r$ _. F+ H
//4、第四次排序，以此内推; m) X! s: }5 Y: H! ~+ v `1 T
//for (int i = 0; i < arr.length - 1 - 1 - 1 - 1 i++) {
8 v2 e" [/ f' H) | // //如果前面的数比后面的数大，则交换
2 p/ A' T: Z) m k1 I9 D // if (arr > arr[i+1]) {
, a* c6 Z# f! g/ ^6 ] // temp = arr;
S* L7 s5 V* W/ V! m // arr = arr[i + 1];
0 W+ b- V a- j# }& }% { // arr[i + 1] = temp;
2 H: g) H c! E# _( a& M# e // }
1 n3 V' O7 R' l& B // }
4 |6 ]0 }7 r$ @$ p" ]+ C int temp = 0;//零时变量，用来将最大的数值排在最后% F: Q5 {7 x0 {
for (int i = 0; i < arr.length - 1; i++) {
! E: U3 X' }% i/ M- j //如果前面的数比后面的数大，则交换
7 a' k( @8 N. H7 O& g if (arr > arr[i+1]) {" M/ l& s8 M6 z; A1 K* ^
temp = arr;
$ @, s9 @. [; Y. H* j: {( K( z- }, m arr = arr[i + 1];) I. W5 N) F0 j9 C/ b
arr[i + 1] = temp;
6 r+ P) ^2 @! N3 i M) c" F }
+ [7 @% P3 w6 u& S) v" B8 h4 W }; A& i$ ^$ F1 e5 a4 W. ^7 X: @
3 \! \2 \: E3 K8 c8 ]8 P# _
0 F/ a4 q# L7 d: }" z+ ~& f9 @
for (int i = 0; i < arr.length - 1 - 1; i++) {& r; q9 C+ d8 j
//如果前面的数比后面的数大，则交换; A; g0 e w% o8 s7 c. T
if (arr > arr[i+1]) {
3 x3 g" o/ D2 R+ n& D( U* L temp = arr;' G5 x: ^0 o+ I' K
arr = arr[i + 1];: v. j F. i9 H1 T
arr[i + 1] = temp;
P+ o4 f7 Z C1 ~) ?' Y0 S }* n' j, [1 {6 r: t% Y7 j: H
}
, ?( V% ?' n+ ~& c" A0 K; f6 z) p% ~/ C
w6 {, c: W+ r! A
for (int i = 0; i < arr.length - 1 - 1 - 1; i++) {( q! k" R9 V' M; ^4 ]* b$ K
//如果前面的数比后面的数大，则交换% `- R; B5 i A, }
if (arr > arr[i+1]) {
. k' H0 ~' ~4 ~/ h' N. @ E temp = arr;
" j. D/ r' s. Z7 j arr = arr[i + 1];
" Q2 @( h C! Z arr[i + 1] = temp;
3 I# I/ P: ^; S! H" k) ]( g }. W" `& D; B5 p9 L, c
}
1 O7 n! c- M8 `4 d" |/ q" k3 G- V7 R I
6 r' }8 [5 D5 _8 X- h3 r, \
for (int i = 0; i < arr.length - 1 - 1 -1 - 1; i++) {+ w& [9 n% _# ~9 e# A9 Z2 k( A' w4 W5 u
//如果前面的数比后面的数大，则交换: W1 n7 V, ~3 \/ S
if (arr > arr[i+1]) {& C/ K5 }3 V6 m# O" ~9 S) l- h
temp = arr;: o i2 @1 }! B" z* J3 P
arr = arr[i + 1];
4 H+ G4 v4 t7 q+ E: L arr[i + 1] = temp;) [8 V+ ^* D) \& n# B
}
8 T4 b5 U g p+ _4 t. d6 l }
: n& r2 h1 F* v; }9 S* Z* ` |
- ?& W! g/ m( ]! K1 g; h9 q
; K" e& R+ b( x$ b8 Y4 F h System.out.println("hello " + Arrays.toString(arr));
3 G( u6 E" X. L //------------------------------------------------------------------------------------' P( c/ C- e+ k s' O4 {, d3 A
//根据上面的观察可以知道了撒，可以再用一套循环解决
: f7 I* _( x7 l5 H0 E- C, t$ g3 |! y# W3 v7 A7 Y
; T) Z' \& R- ?0 x+ R( L7 v- N
" v- K. F+ h" P2 j+ D, y
" Q6 Q' e7 z: S o. y' [& \
//好好理解一下、由此可知，他的时间复杂度为O(n*n)( Y7 N1 R8 b; L, p% h
for (int j = 0; j < arr.length - 1; j++) {
, F& s5 X4 }. r1 s$ R4 J+ O3 A, E for (int i = 0; i < arr.length - 1 - j; i++) {! W% v) ~- R% h
//如果前面的数比后面的数大，则交换
8 O7 I4 a( }' g! z! L0 d1 M& z if (arr > arr[i+1]) {" ]1 W1 O2 z! V) y
temp = arr;
k1 K h$ l' r! E [. Y arr = arr[i + 1];& m b7 q p+ B0 b# x. g5 b
arr[i + 1] = temp;
. n0 A/ _! Q7 |+ T7 @! U }
+ \3 F7 N; h) p; {6 _* Y0 U0 S }% ~6 R" a% n: l* j
}* [ M( c& s+ S8 w4 ]
}
! j1 \5 ~0 T+ T0 k5 _}
! @5 k% e$ ~0 j7 j- _三、冒泡排序的优化1、思路7 J9 p( P0 j+ c1 q' o1 l/ i
如果我们发现在某一糖过程中，没有进行一次交换，提前终止* \! _+ m: d" u$ G& f
2、代码实现
package cn.mldn;
3 V/ ]7 H/ T; u3 p. I4 F! X+ g! G4 t) t
z1 ~/ }8 ?0 {4 y9 himport java.util.Arrays;
+ K0 u( {/ P; \5 @7 `! o! k) l- I8 e" j4 W1 E
: M! _: X5 p. x8 V; d
public class BubbleSort {$ N. c/ C2 T4 N o# b& ?! @
public static void main(String[] args) {
- w. I; z! T) u. z/ `, n int[] arr = {3,9,-1,10,-2};
5 {5 `; L% R5 K6 y$ C //大致过程+ |; X' D; m* ^
//1、第一步就是第一轮排序得到最大值于最后( l# u# L- s. T+ `$ | `" L2 N3 T
// for (int i = 0; i < arr.length - ; i++) {
" C0 ]7 s; }' B' j // //如果前面的数比后面的数大，则交换8 d5 V+ q* x6 ]6 ~ U8 X! o$ W
// if (arr > arr[i+1]) {
; g- v8 K" Q2 A/ o( m# V // temp = arr;( C0 Z/ o5 c& e# [. ^8 O* V k
// arr = arr[i + 1];
5 w9 p, W. o) S- h$ X% v // arr[i + 1] = temp;) _ X' C# K5 x" e& Z+ M9 V& C2 X
// }
. ~$ \4 U. l$ B- ~ // }
( x- p2 h* z/ C0 U: d& S- ^ //2、第二糖就是把倒数第二大的排到倒数第二位
; e4 ?3 x, g/ H; p // for (int i = 0; i < arr.length - 1 - 1; i++) {
! s, w! J. t$ e+ W9 |- e+ ?3 W // //如果前面的数比后面的数大，则交换
" [3 U+ H7 ~( r( a# o // if (arr > arr[i+1]) {
5 v: C* O& _' ~2 S- |2 F; Z) e // temp = arr;
+ G$ Q/ ~1 n, q% D // arr = arr[i + 1];" F% f' \7 k. S" {+ Z
// arr[i + 1] = temp;
: R; }! [& m+ e N% B6 Q: a [) \' e // }; {. ~$ q2 P8 k9 J2 z: o
// }
% X( b8 G0 w* u8 j U& { //3、第三糖排序，以此内推$ s& g" w" }$ W* M
//for (int i = 0; i < arr.length - 1 - 1 - 1; i++) {- u$ h! ?7 N$ p: B8 L3 k) I
// //如果前面的数比后面的数大，则交换
* s( v. {1 R5 a/ I; m0 J // if (arr > arr[i+1]) {
9 r- G0 [2 z# h d$ Q // temp = arr;
8 f) R B* Q; I // arr = arr[i + 1];
) n/ d$ c$ {7 I# X7 `3 }# F, ~2 | // arr[i + 1] = temp;
" K1 j2 p+ u o, S // }, B$ `: w/ \1 Q# o8 d" Y( m; Q5 A4 e
// }! ^# ]6 n4 J6 d9 L. ?
//4、第四次排序，以此内推
2 P. n Q5 E O B6 n //for (int i = 0; i < arr.length - 1 - 1 - 1 - 1 i++) {9 Q1 ]: W/ R# Y* o
// //如果前面的数比后面的数大，则交换
6 M0 U5 }. e/ l/ F& H // if (arr > arr[i+1]) {, s2 e3 y% w2 I( _$ [; u
// temp = arr;
$ `0 v$ X7 N- p, ~ // arr = arr[i + 1];6 h; I2 H' h6 G! t6 @4 i
// arr[i + 1] = temp;
* i' U) U% d# \9 y // }
2 K& z9 O S- u2 d // }
& X! t3 {# N. E /*int temp = 0;//零时变量，用来将最大的数值排在最后
/ L. j' E; ~) r$ Y3 n7 h3 \ for (int i = 0; i < arr.length - 1; i++) {# x0 z0 e6 `0 O T: P, m' ^2 X
//如果前面的数比后面的数大，则交换
7 U# B4 o2 G9 N0 h. j1 n% q' s if (arr > arr[i+1]) {) i6 E% J. t( E3 F; D: _
temp = arr;
3 x8 Y3 O7 l& H# l/ X# F. a arr = arr[i + 1];5 P2 _. t% G6 j1 E" S, R+ v
arr[i + 1] = temp;
% Y: m! p# A' T0 U" k }
+ V1 ]" c8 r, h4 S# j! F1 }- U( j }
) y7 y: r) d& ]! O. V& b& q7 L6 \0 ~: K% ^
; v5 j- C+ N2 \9 Y/ ?
for (int i = 0; i < arr.length - 1 - 1; i++) {; d! B0 S' B1 u
//如果前面的数比后面的数大，则交换# h: q) u( L5 h1 x8 ?
if (arr > arr[i+1]) {
8 j# x# {: ^3 Y8 d @+ g$ S temp = arr;
% Z, \! V* J9 j, y! X; g arr = arr[i + 1];) H' N5 X& N0 w. `( g' o$ N
arr[i + 1] = temp;: [# z, K/ F; R, p
}
5 e5 L% C' o: \ }& W+ Y0 X! i9 x1 [7 N7 x H
" W2 m; D5 a8 j h: N
2 Q t. R. v$ L% l$ b$ t: A
for (int i = 0; i < arr.length - 1 - 1 - 1; i++) {' n! E3 R& B7 i, P1 P7 K
//如果前面的数比后面的数大，则交换9 W! D( B, p8 _2 T
if (arr > arr[i+1]) {
! F. G4 l+ q, G, [5 q temp = arr;
: h" m# n9 c4 _! _0 Y2 J arr = arr[i + 1];+ J1 l8 c/ P4 K2 K1 ~$ j
arr[i + 1] = temp;# {; ~ _7 @* q9 v# R2 u
}# C, p5 z6 I: q: M% r; z
}
! ^7 E/ [& m* B- b, F9 h: R+ _2 R3 q5 a0 c/ p1 ^3 |& @
1 y S/ _- X* \2 ` for (int i = 0; i < arr.length - 1 - 1 -1 - 1; i++) {! ^! O; }. R2 w8 E3 H9 O
//如果前面的数比后面的数大，则交换- {2 R3 `- e$ r+ G: H# N( {: X0 z7 i0 k
if (arr > arr[i+1]) {: e; V4 I/ k' T; s# i3 w& X
temp = arr;" b* |+ i. y1 E3 D7 f
arr = arr[i + 1];" F) k6 J. W& |3 \& P9 i
arr[i + 1] = temp;2 k" E- T/ n5 q- t% A
}8 R4 H5 K2 y0 }, N1 p& t
}*/
, g9 @; Z6 c( O& `5 {2 P1 k9 E! V% G+ I& }8 i$ o0 m+ R2 T4 `
2 B! t( w o6 m8 e
System.out.println("hello " + Arrays.toString(arr));# X; g& I0 s3 R
//------------------------------------------------------------------------------------
: Z# C' h p5 x- X* g. R( A' K //根据上面的观察可以知道了撒，可以再用一套循环解决, r3 Z" q4 R# k
( o' s0 O" Z! d/ x# P% F% C: u0 k$ |8 v7 J1 G4 X- t
1 Z Q a" }, k# D" a, _
$ _1 f q9 D8 Q9 w) w" X4 q1 k O: G! h/ [ |! J) w$ w
2 x- V* x) j1 c4 G //好好理解一下、由此可知，他的时间复杂度为O(n*n)3 B) g: O8 _) C5 @3 m8 k2 L
int temp = 0;' S5 E4 |- x( G7 Z' L( H
2 R$ l% `8 _" `. O8 q- w
' K, e- Y1 @. e! ^. `
boolean flag = false;
, H, }; [1 F- _4 i0 T for (int j = 0; j < arr.length - 1; j++) {
% A& ~9 L) c% J8 w2 @ for (int i = 0; i < arr.length - 1 - j; i++) {
5 |+ x. l! K3 _& F. T8 c# W //如果前面的数比后面的数大，则交换
/ y: {: Y/ v* n; D7 ~ if (arr > arr[i+1]) {0 X0 W. O" T- u. e2 b+ V% ?: l
flag = true;//在这里把flag值为true' W2 L7 T. e u% E$ H% e% ~/ H' t
temp = arr;
2 z$ t6 o) R0 @6 i arr = arr[i + 1];
' n* e& I+ m( J$ X+ l2 y9 j2 U arr[i + 1] = temp;
- j0 _2 g! J, l* W$ I }
0 {; F3 V7 }, G( }3 {' E }
$ k+ k+ w+ O8 S6 l* u, T //在内部循环的时候进行查询# A0 ]: l0 O7 |- p. ~* V+ I) y. [3 g6 ]
if (!flag) {//说明在第一趟排序过程中一次交换都没有发生。
7 y- a \% N( x0 r! M break;
% X( a- v* }7 Y( M7 J } else {
% M& a. X! o6 l* Z flag = false;//没有这个就是执行一遍就没了，要让他进行下次继续
9 F9 T3 V" H2 C0 F }
/ W1 r' S# v( o. p* [5 | }
% G: C, ?; v2 x! t. s Q
" S9 J" W4 m4 G3 R, p {
: O! A5 |7 N+ `4 L: v q System.out.println("world " + Arrays.toString(arr)); r3 I5 A/ M4 A! `! l1 j) [
}
; f! b. R: S6 t8 v; r}' ^- q& U4 e3 X* Y
四、将上面的代码封装为一个方法9 s5 q" V. O& [, R; E
public class BubbleSort { ?# H( C* M5 u
public static void main(String[] args) {5 C& ?2 A2 O5 e$ _0 L; o( t4 Y, L
int[] arr = {3,9,-1,10,-2};
- ~& m: @. i, K2 Y( r* d5 R
1 M1 x: H: n; i, i% `9 M& _# \5 ?0 i6 `( }, K: Q
bubbleSort(arr);
6 e9 G: w0 h; x9 g System.out.println("world " + Arrays.toString(arr));
' R* w$ v6 @% q' R }
& [5 b; ^/ A$ u2 J3 h* Z: ^+ k" t1 c" w; u2 v, V7 o$ s) g% w
) @6 s! A3 z9 k( k) K ^0 j
public static void bubbleSort(int[] arr) {+ Y; i: A# A5 t e6 X2 P
//好好理解一下、由此可知，他的时间复杂度为O(n*n)
/ d5 a! h' n/ `5 Y int temp = 0;4 r* |( y: H% z* t
4 R( A. a9 G3 p
4 i, Q/ t, w% y$ M) k+ W, Z boolean flag = false;
: O4 v+ h% `: m8 B for (int j = 0; j < arr.length - 1; j++) {( y/ L, ]7 y2 y; L4 M# ?
for (int i = 0; i < arr.length - 1 - j; i++) {( I* D5 e& f: C! g+ d4 w9 F
//如果前面的数比后面的数大，则交换& ~8 _/ o( L( Y$ m: K6 V
if (arr > arr[i+1]) {
4 Q- g. K( d# b flag = true;//在这里把flag值为true4 v" @: `1 w) }3 [ Z0 y# ?4 m( W1 Z
temp = arr;
' Q6 ]9 ]1 e5 B ?% r4 ]- a* r arr = arr[i + 1];
" [8 y2 j6 h; y arr[i + 1] = temp;
" x) g. T$ v* R+ S }1 b' A; D1 _# R6 Z b) J; e; O+ P
}& a. L5 \" b$ G! L8 H
//在内部循环的时候进行查询3 f+ ]: I( }! @4 E* q: F$ |& l3 t
if (!flag) {//说明在第一趟排序过程中一次交换都没有发生。' y& e4 E/ c* u
break;% [/ ^9 n& m5 {7 j4 @
} else {
% b) E( ]# f7 a% C& v- w/ [ flag = false;//没有这个就是执行一遍就没了，要让他进行下次继续
: y U! `) N3 Z4 ~" N W }, m; i- y o4 c7 }, x. K! w
}$ g o- K, _; O: G
}
( V* w* \5 x+ `# C2 O+ U}
4 }: ^5 b: e: S* m五、测试一下冒泡排序的时间复杂度1、代码是实现
import java.text.SimpleDateFormat;
c, }) G5 ~: J0 ~0 b1 himport java.util.Arrays;1 E* Y7 k1 w8 L0 |8 i- k
import java.util.Date; F/ U- j% l5 C# k: S; V
# e8 J9 t2 n* f7 Q
9 J+ b5 P! J3 d H" B4 M! Opublic class BubbleSort {
/ E) p' o K1 n1 Q( l# {; J0 l- T& ^ public static void main(String[] args) {# M: O( c& N8 }- |' B1 X$ y9 z
//1、创建80000个数据来测试一下我们的性能
3 `7 A/ d- a9 |7 e9 h2 j int[] arr = new int[80000];# f0 ?3 C1 _0 S
for (int i = 0; i < 80000; i++) {
: X" Z) E X+ E i arr = (int)(Math.random()*80000);//生成0到80000的数5 g% l# _4 M- f, @
}; L; u9 k( h" h) _( ]( [
//2、输出时间
0 g/ R3 a2 ?7 Y/ i Date date1 = new Date();
0 \3 g; D9 B0 v( d v- J/ B& @ SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-mm-dd HH:mm:ss");//格式化
' q' y F0 o$ C String date1Str = simpleDateFormat.format(date1);: k& y) D9 g0 \+ s/ [2 f
System.out.println("排序前的时间" + date1Str);) F6 x1 {, q. k3 }
bubbleSort(arr);; { x, J+ S e/ F2 T: p
Date date2 = new Date();
5 g' h8 a, {7 S% H8 r0 ^% _7 Y String date2Str = simpleDateFormat.format(date2);' b8 [% K' B0 J# B
System.out.println("排序后的时间" + date2Str);; C# n- G( t2 g2 K) T
8 B5 U# v+ [ z$ Y/ _( O, g( F$ j
, R6 H2 Y1 h) z7 g$ ^; V) g8 k# G
, d2 x2 ?) ?3 R
( d; o& h' O2 u3 M# w6 L4 } }! I3 i( l: ^) Z, J9 _' p' h( y
( o/ `2 f1 W' V1 X5 P/ x3 A" O' y. |
2 Q, z9 m$ q' E% a9 V
public static void bubbleSort(int[] arr) {
' b3 Q8 X: i4 o! l6 `: b //好好理解一下、由此可知，他的时间复杂度为O(n*n)
$ t3 ?3 Q) [" R( `6 V1 K: F3 }- l int temp = 0;
0 q- H. u/ o7 N* A
# U7 ~# y# |% Z3 v& y6 S9 O" V3 @+ h/ Z
boolean flag = false;
$ o3 g. l/ P% l% I for (int j = 0; j < arr.length - 1; j++) {7 [9 o: e* v2 z; g- x
for (int i = 0; i < arr.length - 1 - j; i++) {9 X2 @) G; |! L; K
//如果前面的数比后面的数大，则交换
) K2 ~' w- J) \ if (arr > arr[i+1]) {
5 I8 _6 v: D6 O1 `0 v: U9 @# y3 Q flag = true;//在这里把flag值为true
5 Z, m; ]8 P$ b, J/ l3 j; O* X* Z temp = arr;
) K! N5 c8 Y/ O7 y8 O+ a arr = arr[i + 1];
4 x$ D; w0 ^9 N# J- f3 i" b arr[i + 1] = temp;
0 m1 C, D E) _3 q m }$ V6 M; a3 C! D+ _
}8 M6 J1 J( A% I5 @- d* c
//在内部循环的时候进行查询. v& I" s4 y) ^/ ^
if (!flag) {//说明在第一趟排序过程中一次交换都没有发生。- G# z9 Y( _3 O" T
break;% r0 N ]% n; Z/ g$ c5 U) c
} else {
; e/ G Y% X3 C7 T# Y3 O7 | flag = false;//没有这个就是执行一遍就没了，要让他进行下次继续
8 f7 l% O- _/ x/ B }
" Y1 N0 Q" b4 p C" _ }0 Y/ \" @ y" {! F% Z& Q0 c- L6 e0 Z
}
( X% E. v' ~( k. C3 _! I7 F! k) N2 o}
5 {. n" Z) S5 N6 z
, y1 j$ c, s! B# E% }) J: d
$ E7 A! `$ o2 P5 x# B1 L
& E2 p; ` V7 j8 n$ L6 f: }. F2 T2、效果8 S0 Y& N/ a4 v/ _
" o) V' s% ^$ A+ }# ^7 x6 y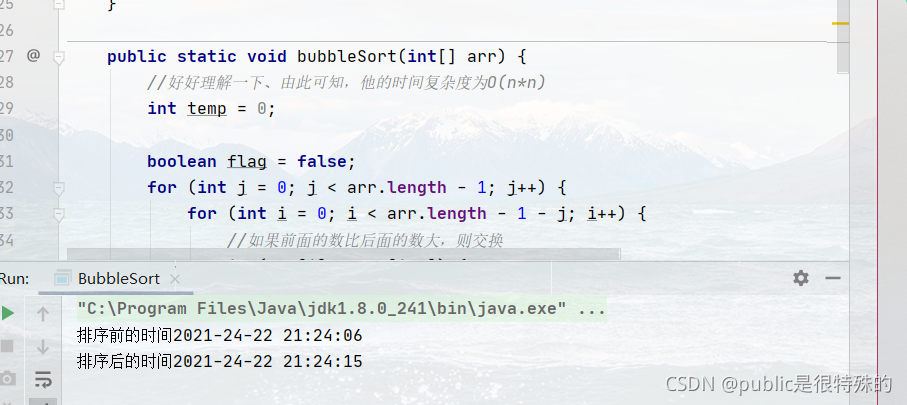
C) \) w4 J" g8 Q8 J( U
1 N: S# a. E3 q6 I; l0 @2 F
3 _8 n) v: E+ A1 ?5 J3 B- D
# k# t$ O- V1 T; U( Q
作者: 470557092 时间: 2021-10-29 21:15
顶。。。。。。
- Z/ k+ K2 q) O; [. I! W
6 M) x9 C, d: U! W2 {; o* g2 S
| 欢迎光临 数学建模社区-数学中国 (http://www.madio.net/) |
Powered by Discuz! X2.5 |