不少朋友给我发邮件或留言询问关于蒙特卡罗算法，我在与他们的交流过程中发现大部分朋友对这算法似懂非懂，特别是对它的原理基本上不了解，一个原因是他们中大部分人的数理统计知识不够，特别是对条件密度函数推导和大样本渐进收敛（中心极限定理）相当陌生。这里我尽量用简单的语言叙述一下用蒙特卡罗方法计算积分的原理。

 

理论知识：

 

1、密度函数

     对于连续型随机比变量X，分布函数F(x)描述了它的分布特性，而密度函数f(x)是分布函数的微分，满足如下一些条件：

 

2、期望

     连续型随机变量的期望为如下的定积分（注意许多研究问题的核心就是计算某个定积分）：

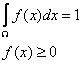
3、总体和样本，总体是指抽样的全体，样本指从总体中抽取的部分。比如从一个班的全体学生身高中抽取4个学生的身高，其中“一个班的全体学生身高”叫做总体，“4个学生的身高”叫做样本，“4”叫做样本容量。总体服从某种分布，比如一个班级学生的身高服从正态分布N(MIU,SIGMA)，通常样本是从总体中独立抽样得到的，称它们之间独立同分布（i.i.d）。总体的均值叫期望记做E(X),计算方法如2所示。样本均值计算公式为：

总体的均值通常不知道，这时候可以用样本均值替代总体均值，称“用本均值估计总体均值”

4、抽样：从总体中抽取若干个样本值。在蒙特卡罗计算中，抽样过程即从指定分布中产生（伪）随机数的过程。

蒙特卡罗积分原理：

        有了以上几个概念，就能看懂蒙特卡罗的原理了：计算某个函数g(x)的积分，则将选择一个概率密度函数（理论上讲可以在积分区间上任意选择一个概率分布），然后做如下代数处理：

上式左边是一个积分，右边化成了两个函数比值的样本均值，用样本均值去估计总体均值（期望，也就是待求的积分），这就是蒙特卡罗积分的原理。从选定的概率分布f(x)中抽样，多次（相当多）抽样后，带入式子g(xi)/f(xi)，然后计算样样本的均值，它近似地等于待求的积分。

关于蒙特卡罗积分的精度分析，涉及到中心极限定理，我将在下一篇中写出来。