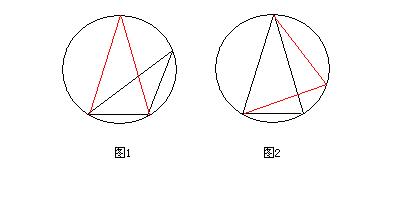
容易看出，在同底的内接三角形中，等腰三角形面积最大。如图1，等腰三角形的高是直径的一部分，在所有同底的三角形中最大，所以面积也是最大的。这个结论容易得出，下一步怎么办呢？看看一个等腰三角形，如图2，如果不是等边的话，以其腰为底，再作一个内接等腰三角形，这两个等腰三角形不会重合，根据前面的道理，后作的等腰三角形面积更大（其高是直径的一部分）。因此对于任意一个内接三角形如果不是等边三角形，总可以找到另一个三角形面积比它大。得到这个结论后，可以用反证法来证明等边三角形面积是最大的。假设等边三角形面积不是最大的，则存在另一个三角形面积最大，根据前面的结论，又可找到另一三角形面积比它更大，这就产生了矛盾，因此等边三角形面积是最大的。

       对于圆的一个内接等腰三角形，以其腰为底再作一个内接等腰三角形，后者的面积更大，再以后者的腰为底作一个等腰三角形，其面积更大，这样的过程可以无限进行下去。三角形的面积一个比一个大，但又有上限，比如小于圆的面积，因此有一个极限值，就是等边三角形的面积。实际上不断的作等腰三角形就可得到最大面积的内接三角形。

       这道题目的解答和一首唐诗很像，是哪一首呢，就是那首我们都很熟悉的王之涣的《登鹳雀楼》。

              “白日依山尽，

               黄河入海流。

               欲穷千里目，

               更上一层楼。”

       这首诗人们从中读到了色彩，读到了意境，现在又可读到数学。

      “日”的形状是什么？是一个圆。

      “山”的形状是什么？可以是一个三角形。

      “白日依山尽”，意味着一个圆和一个内接三角形。

      “欲穷千里目”，意是看到最远的地方，可以想象为要找到一个面积最大的三角形。

      “更上一层楼”，是指达到目标的方法，在这个数学题目里方法就是找到更大的一个等腰三角形，再不断的找下去，和“更上一层楼”非常的相似。

      “欲穷千里目，更上一层楼”可以说是求极限。

       数学题和唐诗是不是很相象？