风马牛不相及

       “风马牛不相及”是我们熟知一个成语，出自《左传·僖公四年》：“君处北海，寡人处南海，唯是风马牛不相及也。”

        两百多年前，法国科学家布丰请了许多客人到家里作了一次试验。他在一张纸上画了一些平行线，拿出了一包事先准备好的小针，让客人把小针往纸上扔，并让客人告诉他针是否和平行线相交。客人们不知道他葫芦里卖的是什么药，按照他的意思不停的扔小针，布丰在一旁记录。如此这般，小针投了很多次，最后布丰对大家说：根据记录共投针2212次，其中与平行线相交704次，两者之比为3.142，这就是圆周率π的近似值！当时全体哗然，不明白投针怎么就投出一个π来。

       平行线，投针，圆周率π，风马牛不相及吧？ 这里面究竟是怎么一回事呢？

       布丰纸上的平行线、小针的长度是有讲究的，平行线间的距离都相等，小针的长度恰为这个距离的一半。

       假设平行线间的距离为a，针的长度为l，a>l，针扔到纸上，要么和平行线不相交，要么和一条线相交有一个交点。一个硬币投到地面要么是正面，要么是反面，每面的概率是1/2，但针投到纸上和一条线相交的概率却不是1/2，是多少？可以计算。

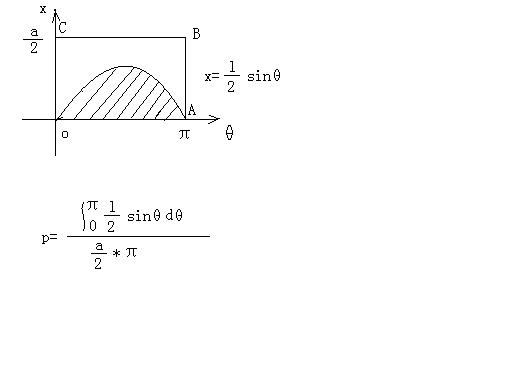
      设x为针中点到最近一条平行线的距离，则0≦x≦a/2，

      设θ是针与平行线间的夹角，则0≦θ≦π，

      当θ一定，在0≦x≦1/2·sinθ时，针与平行线相交，

                     在1/2·sinθ<x≦a/2时，针与平行线不相交，

     当θ从0到π变化时，根据下面的图就可计算相交的概率p,

    P=(阴影区面积)/(矩形OABCD面积)

       算出p=2·l/a·π

       因此π＝2·l/a·p

      在投针次数m较多时，如相交的次数为n，则p约为n/m，而l为a的一半时，π约为m/n，这就是投针求π的道理。